द्विघात समीकरण कक्षा 10 गणित
भूमिका
बच्चों हमने पिछले अध्याय बहुपद मे बहुपदीय समीकरण के बारे मे पढ़ा है, तो हम कह सकते है वह बहुपदीय समीकरण जिसमे चर की अधिकतम घात 2 होती है द्विघातीय समीकरण कहलाता है तथा साथ मे एक घात के चर तथा अचर पद हो सकते है। जिसका मानक समीकरण ax2+bx+c=0 जहाँ a≠0 अनिवार्य है तथा a, b क्रमशः x2, x के गुणांक व c अचर पद है।
इस अध्याय मे हम द्विघात समीकरण, द्विघात समीकरण के प्रकार, गुणन खंड विधि द्वारा द्विघात समीकरण के हल, पूर्ण वर्ग बनाकर हल करने की विधि, द्विघात सूत्र द्वारा द्विघात समीकरण का हल ज्ञात करना तथा द्विघात समीकरण के मूलों की प्रकृति का अध्ययन करेंगे।
आइये जानते है द्विघात समीकरण को और करीब से....
हैलो बच्चों, पिछले अध्याय बहुपद मे हमने एक घातीय, द्विघातीय, त्रिघातीय आदि बहुपदो को जाना था, बहुपद के प्रकार का चयन हम उसके चर के अधिकतम घात से करते है। अतः ऐसा बहुपद जिसमे चर की अधिकतम घात 2 होती है द्विघातीय बहुपद कहलाता है। द्विघात बहुपद का व्यापक रूप P(x)=ax2+bx+c,a≠0 के रूप का होता है। जहाँ a,b,c वास्तविक संख्याएँ है ,जो द्विघात बहुपद के गुणांक कहलाते हैं।
किसी द्विघातीय बहुपद का ज्यामितीय रूप परवलय के आकार का होता है। नीचे दिए चित्र को देखे 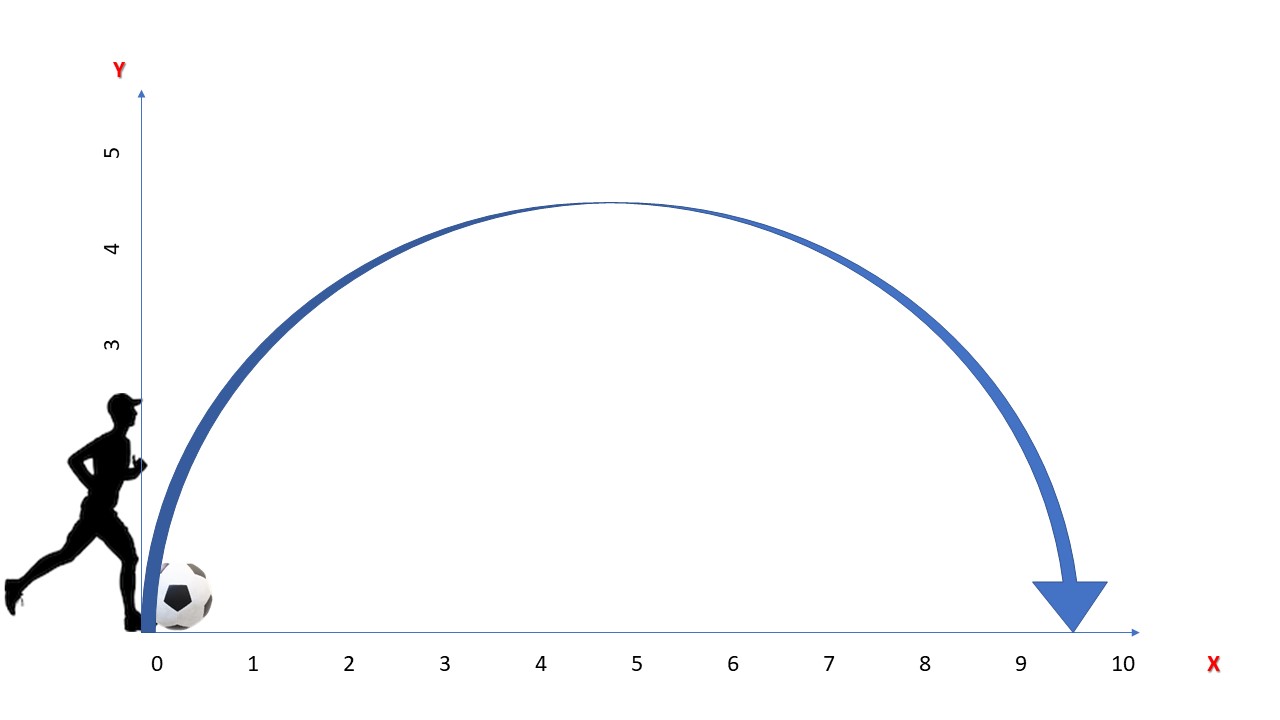
चित्र में एक फुटबॉल का खिलाडी जब फुटबॉल को मारता है तो फुटबॉल हवा में जिस पथ का अनुसरण करती ऐसे पथ को परवलयाकार पथ कहते है। इसी प्रकार आप व्यावहारिक जीवन में अपने आस-पास ऐसे अनेको उदाहरणों को देख सकते है।
एक द्विघात बहुपद परवलयाकार पथ के बिंदुओं का बिंदुपथ होता है। यहाँ चित्र मे आपने देखा होगा बॉल x− अक्ष मे आगे की ओर तथा y− अक्ष (y=P(x)) मे ऊपर व नीचे की ओर जा रहा है।
(यहाँ आगे शून्यक को समझने का प्रयास करेंगे।)
अब आप देखिये की यहाँ y- अक्ष का मान 0 कहाँ आ रहा है? अर्थात P(x)=0 कहाँ मिल रहा है?
- यहाँ हम देख सकते है कि जब बॉल जमीन पर होगा तब y=0 अर्थात P(x)=0 प्राप्त होगा और चित्र मे ऐसा 2 बार हो रहा है।
एक बार जब बॉल को मारा जाता है तथा दूसरी बार जब बॉल जमीन पर गिरता है।
यदि p(k)=0 तब x=k , P(x) का शून्यक है।
आइए इसका एक उदाहरण देख लेते है
यदि P(x)=x2−x−6........(i)
तब P(x)=(x+2)(x−3).....(ii)
हल करने पर
समीकरण (ii) से x = -2 रखने पर
P(−2)=(−2+2)(−2−3)=0 प्राप्त होगा।
इसी प्रकार
P(3)=(3+2)(3−3)=0 प्राप्त होगा ।
यहाँ देख सकते है की x=−2 व x=3 पर P(x) का मान शून्य प्राप्त हो रहा है , यहाँ से देख सकते है की 2 स्थानों पर P(x) शून्य प्राप्त हुए अतः 2 शून्यक प्राप्त हुआ,
आइए समीकरण (i) मे विभिन्न मान रखकर देखते है की कौन सा वक्र प्राप्त होगा
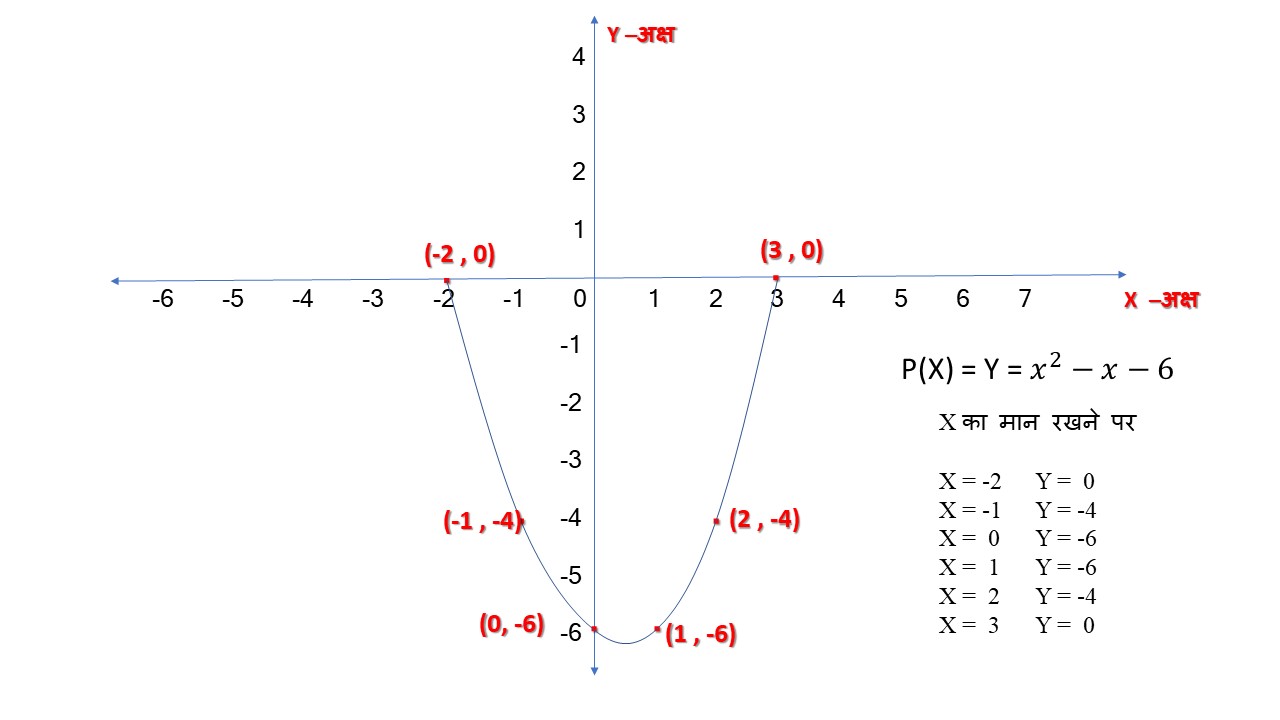
जैसा की हमने कहा था यहाँ एक परवलय प्राप्त हुआ।
किसी द्विघातीय बहुपद को यदि शून्य के तुल्य लिखा जा सके तब उस प्राप्त समीकरण को द्विघातीय समीकरण कहते है। इस अध्याय में हम द्विघात समीकरणों को जानेंगे तथा उनको हल करने की विधियों तथा उनके मूलों (शून्यको) की प्रकृति के बारे में जानेंगे।
1. द्विघात समीकरण
यदि a,b,c वास्तविक संख्याएँ हों तथा a≠0 (अन्यथा a=0 करने पर यह एक घातीय रेखीय समी० हो जायेगा) तो ax2+bx+c=0.........(i) के रूप का कोई भी समीकरण द्विघात समीकरण कहलाता है।
जैसे की
- 4x2−3x−5=0
- 2x2+9x+8=0
- x2−3x=10
- (2x+3)(3x−7)=0
इस प्रकार p(x)=0 के रूप का कोई समीकरण है, जहाँ p(x) घात 2 का एक बहुपद है, x में एक द्विघात समीकरण होता है।
बच्चों यहाँ ध्यान देने योग्य बात यह है की समीकरण (i) मे b=0 या c=0 होने पर भी यह एक द्विघातीय समीकरण होगा।
बच्चों अब आगे हम सीखेंगे द्विघात समीकरण की जाँच करना, जैसा की अभी आपने सिखा कि यहाँ a≠0 होना चाहिए, चूँकि यहाँ सबसे महत्वपूर्ण यह है की समीकरण मे 2 घात वाला चर अवश्य हो साथ ही समीकरण की अधिकतम घात 2 हो। यह बातें ध्यान मे रखकर हम आसानी से द्विघात समीकरण की पहचान कर सकते है।
उदाहरण 1
निम्नलिखित में से कौन सी द्विघात समीकरण है?
(i) 3x2+6=0 (ii) x+1x=2 (iii) x2+1x+3=0
(i) स्पष्ट है की 3x2+6 एक द्विघात बहुपद है
इसलिए 3x2+6=0 एक द्विघात समीकरण है।
(ii) x+1x=2
⇒x+1x−2=0
⇒x2+1−2xx=0
⇒x2−2x+1=0
स्पष्ट है की x2−2x+1 एक द्विघात बहुपद है।
अतः x2−2x+1=0 एक द्विघात समीकरण है।
(iii) x2+1x+3=0
⇒x3+3x+1=0
स्पष्ट है की x3+3x+1 एक त्रिघातीय बहुपद है,
इसलिए दी गई समीकरण द्विघात समीकरण नहीं है।
उदाहरण 2
एक रेलगाड़ी समरूप चाल से 480 किमी की दुरी तय करती है यदि उसकी चाल 8 किमी / घंटा कम होती तो उसे दुरी को तय करने में 3 घंटे अधिक समय लगता इस स्थिति को द्विघात समीकरण के रूप में प्रकट करे
ट्रेन द्वारा तय की गई दुरी=480 किमी
मान लीजिये की ट्रेन की चाल =x किमी / घo
अतः 480 किमी तय करने में ट्रेन को लगा समय =480x घंटे
यदि ट्रेन की चाल 8 किमी / घo कम हो अर्थात (x−8) होती
तब 480 km तय करने में ट्रेन को लगा समय =
480x−8
अतः 480x−8−480x=3
480x−480(x−8)x(x−8)=3
या 480x−480(x−8)=3x(x−8)
या 480x−480x+3840=3x2−24x
या x2−8x−1280=0
यही अभीष्ट द्विघात समीकरण है
2. द्विघात समीकरण के प्रकार
द्विघात समीकरण के दो प्रकार होते हैं:
- शुद्ध द्विघात समीकरण
- मिश्रित द्विघात समीकरण
(1) शुद्ध द्विघात समीकरण-
जिस द्विघात समीकरण में चर x का एक घात वाला पद नहीं हो उसे शुद्ध द्विघात समीकरण कहते है| अर्थात यदि द्विघात समीकरण ax2+bx+c=0 में b=0 हो तो वह शुद्ध द्विघात होगा| ऐसे समीकरणों का व्यापक रूप ax2+c=0 होता है, जहाँ a≠0 होना आवश्यक है।
उदाहरण -
- (i) x2−9=0
(ii) 25t2=64
(2) मिश्रित द्विघात समीकरण -
जिस द्विघात समीकरण में चर x का एक घात वाला पद भी हो उसे मिश्रित द्विघात समीकरण कहते हैं। स्पष्ट है कि मिश्रित समीकरण का व्यापक रूप ax2+bx+c=0 होता है, जहाँ a≠0,b≠0 होना आवश्यक है।
उदाहरण -
- (i) x2+3x+2=0
द्विघात समीकरणो को हल करने की विधियाँ
द्विघातीय समीकरणों को 3 प्रकार से हल किया जा सकता है -
- गुणनखंड विधि
- पूर्ण वर्ग बनाकर हल करने की विधि
- द्विघातीय सूत्र (श्री धराचार्य सूत्र)
3. गुणन खंड विधि द्वारा द्विघात समीकरण के हल
अब बच्चों जैसे की यदि 6 का गुणनखंड करे तो हमे 3×2 प्राप्त होगा, यहाँ 3 व 2 , 6 के गुणनखंड है। इसी प्रकार द्विघात समीकरण के गुणनखंड निकलेंगे आइए इस विधि को समझ लेते है -
नीचे एक द्विघात समीकरण दिया गया है -
x2+(a+b)x+ab
⇒ x2+ax+bx+ab
यहाँ प्रारंभ के दो पदों व अंत के दो पदों से क्रमशः x तथा b बाहर निकाल सकते है तब
⇒ x(x+a)+b(x+a)
= (x+a)(x+b) प्राप्त होगा।
यहाँ (x+a) तथा (x+b) गुणनखंड प्राप्त हुए
यहाँ तक आप गुणनखंडों को समझ गए होंगे।इस विधि को उदाहरण से समझने का प्रयास करते है -
गुणनखण्डन द्वारा शुद्ध द्विघात समीकरण को हल करना-
उदाहरण -
(i) 4x2−9=0
⇒(2x)2−32=0
⇒(2x+3)(2x−3)=0
(चूँकि a2−b2=(a+b)(a−b))
अब दोनों प्राप्त गुणनखंडो को अलग -अलग शून्य के बराबर रखने पर
2x+3=0
⇒x=−32
2x−3=0
⇒x=32
अतः x=32 , x=−32
द्विघात समीकरण के गुणनखंड विधि द्वारा प्राप्त हल है
गुणनखण्डन द्वारा मिश्रित द्विघात समीकरण को हल करना -
उदाहरण -
(ii) x(7x+3)=4
STEP-1 सबसे पहले दिए गए समीकरण को द्विघात समीकरण के व्यापक रूप (ax2+bx+c=0) में बदलते है :
7x2+3x−4=0
STEP-2 मध्य पद को इस प्रकार विभक्त करे कि :
चर x के गुणांकों का गुणनफल = चर x2 का गुणांक × अचर पद
7x2+(7x−4x)−4=0
अतः x के गुणांकों का योग (7+(−4)=3) 3 के बराबर तथा गुणनफल 7×(−4) है जो की बराबर है चर x2 का गुणांक × अचर पद = 7×(−4) के
(माना पहला पद =7x, दूसरा पद =4x)
⇒7x2+7x−4x−4=0
⇒7x(x+1)−4(x+1)=0
=>(7x−4)(x+1)=0
STEP-3 अब दोनों प्राप्त गुणनखंडो को अलग-अलग शून्य के बराबर रखने पर
7x−4=0⇒x=47
x+1=0⇒x=−1
द्विघात समीकरण के गुणनखंड विधि द्वारा प्राप्त हल है।
उदाहरण 3
द्विघात समीकरण x2−2x−3=0 को हल कीजिए।
दिया है,
x2−2x−3=0
⇒x2−3x+x−3=0
⇒x(x−3)+1(x−3)=0
⇒(x−3)(x+1)=0
⇒x=3,−1
उदाहरण 4
3 वर्ष पूर्व रहमान की आयु का व्युत्क्रम और अब से 5 वर्ष पश्चात् आयु के व्युत्क्रम का योग 13 है। उसकी वर्तमान आयु ज्ञात कीजिए।
माना की बच्चे की वर्तमान आयु x वर्ष है।
3 साल पूर्व, बच्चे की आयु =
(x -3) वर्ष
5 साल बाद उसकी आयु =
(x +5) वर्ष
दिए गए अनुसार,
1x−3+1x+5=13
⇒x+5+x−3(x−3)(x+5)=13
⇒2x+2x2+2x−15=13
⇒x2−4x−21=0
⇒x2−7x+3x−21=0
⇒x(x−7)+3(x−7)=0
⇒(x−7)(x+3)=0
⇒x=7
या x=−3
चूँकि आयु ऋणात्मक नहीं हो सकती, इसलिए x = 7
अतः बच्चे की वर्तमान आयु =7 वर्ष
OMR (One Minute Revision)
गुणनखण्डन द्वारा मिश्रित द्विघात समीकरण को हल करना -
STEP-1 सबसे पहले दिए गए समीकरण को द्विघात समीकरण के व्यापक रूप (ax2+bx+c=0) में बदलते है
STEP-2 मध्य पद को इस प्रकार विभक्त करे कि :
चर x के गुणांकों का गुणनफल = चर x2 का गुणांक × अचर पद
STEP-3 अब दोनों प्राप्त गुणनखंडो को अलग-अलग शून्य के बराबर रखेंगे
4. पूर्ण वर्ग बनाकर हल करने की विधि
आइए इसे एक उदाहरण से समझते है ,
यदि हमारे पास कोई समीकरण 2x2+3x=0 हो तब
सबसे पहले इसका हल गुणनखंड विधि से देखते है ।
अब यदि इसमे से x बाहर निकाल दे तो
x(2x+3)=0 मिलेगा ,
अतः x=0 तथा x=−32 प्राप्त होगा ।
अब बच्चों इसे पूर्ण वर्ग करके हल करने की विधि से हल करेंगे -
(i) सबसे पहले यह x2 का गुणांक 1 लाना होगा इसके लिए पूरे समीकरण को 2 से भाग दे देंगे
x2+(32)x=0.......(i)
प्राप्त होगा
(ii) चूँकि
a2+2ab+b2=(a+b)2
∴ समीकरण (i) को इसी रूप मे लाने का प्रयास करते है ,
यहाँ मध्य पद मे 2 का गुणा व भाग करने पर
x2+2(34)x=0
प्राप्त होगा ।
(iii) इसे आगे पूर्ण वर्ग बनाना है इसलिए
यहाँ
a=x व
b=34 ले तब
a2+2ab+b2=0 के रूप मे समीकरण को लाने के लिए (34)2 को जोड़ने व घटाने पर
x2+2(34)x+(34)2−(34)2=0
⇒ (x+34)2−(34)2=0
∴ x+34=±34
⇒ x=0 तथा −32 प्राप्त हुआ ,
जो कि सही है ।
उदाहरण 5
द्विघात समीकरण 9x2−15x+6=0 को पूर्ण वर्ग बनाने वाली विधि द्वारा हल कीजिए।
यहाँ दिया है,
9x2−15x+6=0
⇒x2−159x+69=0
⇒x2−53x+23=0
⇒x2−53x=−23
⇒x2−2(56x)=−23
⇒x2−2(56)x+(56)2
=(56)2−23
⇒(x−56)2=2536−23
⇒(x−56)2=25−2436
⇒(x−56)2=136
⇒x−56=±16
⇒x=56±16
⇒x=56+16=1
(धन चिह्न )
या x=56−16=23
(ऋण चिह्न )
⇒x=1 या 23
उदाहरण 6
4x2−3x−1=0 को पूर्ण वर्ग बनाकर हल कीजिए।
दिया है, 4x2−3x−1=0
⇒4(x2−34x)=1
⇒x2−34x=14
⇒x2−34x+(38)2
=14+(38)2
⇒(x−38)2=14+964
=2564=(58)2
⇒x−38=±58
⇒x=38±58
⇒x=38+58=1
('+' चिह्न लेने पर)
तथा x=38−58
⇒x=−14
('-' चिह्न लेने पर)
अतः दी गई समीकरण का हल (1,−14) है।
OMR (One Minute Revision)
पूर्ण वर्ग विधि द्वारा समीकरण को हल करना -
STEP-1 सबसे पहले समीकरण में x2 का गुणांक 1 करेंगे
STEP-2समीकरण को a2+2ab+b2=(a+b)2
रूप मे लाने का प्रयास करते है
STEP-3 इसे आगे पूर्ण वर्ग बनाना है
5. द्विघात सूत्र द्वारा द्विघात समीकरण का हल ज्ञात करना
बच्चों इससे पहले आपने पूर्ण वर्ग करके किसी द्विघात समीकरण का हल करने की विधि को समझा इसी विधि कि सहायता से हम द्विघात सूत्र की उपपत्ति करते है
मान लीजिए कि
ax2+bx+c=0,a,b,c∈R
और a≠0 एक द्विघात समीकरण है |
अब, ax2+bx+c=0
[ दोनों पक्षों को a से भाग देने पर ]
∴ x2+bax+ca=0
[दोनों पक्षों में b24a2 जोड़ने पर ]
या, x2+2.xb2a+b24a2+ca=0+b24a2
या, x2+2.xb2a+b24a2=b24a2−ca
या, x2+2.b2ax+(b2a)2
=b24a2−ca
या, (x+b2a)2=b2−4ac4a2
दोनों पक्षों का वर्गमूल लेने पर हमें मिलता है,
x+b2a
=±√b2−4ac4a2
=±√b2−4ac2a
∴x=−b2a±√b2−4ac2a
=−b±√b2−4ac2a
द्विघात समीकरण के मूलों को ज्ञात करने के लिए प्राप्त उपर्युक्त सूत्र को द्विघात सूत्र कहा जाता है तथा इस नियम को प्राचीन भारतीय गणितज्ञ के नाम पर श्रीधराचार्य का नियम कहा जाता हैं |
अतः समीकरण
ax2+bx+c=0
को संतुष्ट करने वाले x के मान,
−b−√b2−4ac2a
और −b+√b2−4ac2a हैं |
b2−4ac को द्विघात समीकरण ax2+bx+c=0,
का विविक्तकर कहते हैं और इसे D से सूचित करते हैं|
इस तरह द्विघात समीकरण
ax2+bx+c=0
के मूल α और β हैं,
जहाँ α=−b−√D2a
और β=−b+√D2a,
जहाँ D=b2−4ac
उदाहरण 7
दत्त समीकरण
(x−2x+2)2+3−4x−2x+2=0 x≠−2
को हल कीजिये
मान लीजिये
y=x−2x+2
तब दत्त समीकरण हो जाता है
y2+3−4y=0
या y(y−3)−1(y−3)=0
⇒ (y−1)(y−3)=0
⇒y=1,3
अब y=1
→x−2x+2=1
⇒ x−2=x+2
यह संभव नहीं है
पुन y=3
→x−2x+2=3
⇒x−2=3x+6
⇒ 2x=−8
→x=−4
इस तरह x=−4 अभीष्ट हल है ।
उदाहरण 8
द्विघात सूत्र का प्रयोग करके, निम्नलिखित समीकरण को हल कीजिए।
a2b2x2−(4b4−3a4)x−12a2b2=0
दिया है,
a2b2x2−(4b4−3a4)x−12a2b2=0
अब, दी गई समीकरण की तुलना
Ax2+Bx+c
से करने पर,
A=a2b2,
B=−(4b4−3a4)
=(3a4−4b4)
और C=−12a2b2
∴D=(B2−4AC)
- =(3a4−4b4)2−4a2b2(−12a2b2)
=9a8+16b8−24a4b4+48a4b4
=9a8+16b8+24a4b4
=(3a4)2+(4b4)2+2×3a4×4b4
=(3a4+4b4)2≥0
चूँकि, दी गई समीकरण के मूल वास्तविक हैं।
अतः
α=−B+√D2A
- =(4b4−3a4)+(3a4+4b4)2a2b2
=8b42a2b2
=4b2a2
और
β=−B−√D2A
- =(4b4−3a4)−(3a4+4b4)2a2b2
=−6a42a2b2
=−3a2b2
इसलिए 4b2a2 और −3a2b2 दिए गए समीकरण के अभीष्ट मूल हैं।
6. द्विघात समीकरण के मूलों की प्रकृति
हमने देखा है कि α और β
द्विघात समीकरण ax2+bx+c=0
के मूल हैं,
जहाँ
α=−b−√b2−4ac2a
और β=−b+√b2−4ac2a …(i)
Case - I.
जब b2−4ac<0 :
हम जानते हैं कि वास्तविक संख्या का वर्ग ऋणात्मक नहीं होता है| अतः किसी ऋणात्मक संख्या (b2−4ac) का वर्गमूल एक वास्तविक संख्या नहीं हो सकता है| अतः यदि b2−4ac<0 तब √b2−4ac वास्तविक संख्या नहीं होगा|
इसलिए (i ) से यह स्पष्ट है कि α और β वास्तविक नहीं होंगे अर्थात
द्विघात समीकरण के मूल वास्तविक नहीं होंगे यदि b2−4ac<0.
Case - II.
जब b2−4ac=0 :
यदि b2−4ac=0
तो √b2−4ac=0
अतः (i ) से
α=−b2a
और β=−b2a,
अर्थात α=β.
इस तरह हम देखते हैं कि जब b2−4ac=0 तब मूल वास्तविक और समान होंगे
और प्रत्येक मूल −b2a होगा|इस स्थिति में मूलों को पुनरावृत्त मूल कहते हैं|
Case III.
जब b2−4ac>0 :
यदि b2−4ac>0,
तब √b2−4ac एक वास्तविक संख्या होगी
और √b2−4ac>0 होगी|
मान लें कि √b2−4ac=k
तब (i) से,
α=−b−k2a
और β=−b+k2a
स्पष्टतः α और β भिन्न हैं
चूँकि k≠0
यदि b2−4ac>0 तो द्विघात समीकरण के मूल वास्तविक और भिन्न होते हैं|
(b2−4ac) को द्विघात समीकरण ax2+bx+c=0 का विविक्तकर (विवेचक) कहते हैं। विविक्तकर को सामान्यतः D या Δ से सूचित किया जाता हैं , जैसा की हम जानते है विविक्तकर(discriminant) से तात्पर्य भिन्न करना या अलग करना या अलग गुण बताने से है । चूँकि b2−4ac के प्रकृति पर मूलों की प्रकृति निर्भर करेगी, इसलिए b2−4ac विविक्तकर कहलाता है।
OMR (One Minute Revision)
किसी द्विघात समीकरण के अधिकतम 2 शून्यक/ मूल हो सकते है।
यदि α व β द्विघात समीकरण ax2+bx+c=0 के दो मूल है तो
α=−b−√D2a और β=−b+√D2a
जहाँ D=b2−4ac द्विघात समीकरण का विवेचक या विविक्तकर कहलाता है।
विविक्तकर (D) के आधार पर निम्न तीन स्थितियां संभव है
- स्थिति 1− जब D<0 तब द्विघात समीकरण के कोई वास्तविक शून्यक प्राप्त नहीं होते।
स्थिति 2− जब D=0 तब द्विघात समीकरण के वास्तविक तथा समान शून्यक प्राप्त होते है।
स्थिति 3− जब D>0 इस स्थिति में द्विघात समीकरण के वास्तविक तथा असमान शून्यक प्राप्त होते है।
उदाहरण 9
समीकरण 3x2−2x+13=0 का विविक्तकार ज्ञात कीजिए और फिर मूलों की प्रकृति ज्ञात कीजिए| यदि वे वास्तविक है, तो उन्हें ज्ञात कीजिए |
द्विघातीय मानक समीकरण
a2+bx+c=0
से दिए गए समीकरण की तुलना करने पर
यहाँ a=3, b = -2, c=13 है|
इसलिए विविक्तकर
b2−4ac
=(−2)2−4×3×13
=4−4=0 है|
अतः द्विघात समीकरण के दो बराबर वास्तविक मूल है|
ये मूल −b2a,−b2a
अर्थात
26,26,
अर्थात
13,13 है|
उदाहरण 10
k का वह मान ज्ञात कीजिए जिसके लिए द्विघात समीकरण (k+4)x2+(k+1)x+1=0 के मूल वास्तविक तथा बराबर हैं।
दी गई समीकरण की तुलना
Ax2+Bx+C=0
से करने पर,
A=k+4,B=k+1 और C=1
∴D=B2−4AC
⇒D=(k+1)2−4(k+4)
D=k2+2k+1−4k−16
D=k2−2k−15
D=(k−5)(k+3)
यदि दी गई समीकरण के मूल वास्तविक हैं,
तब D=0
⇒(k−5)(k+3)=0
⇒k=5,−3
उदाहरण 11
यदि समीकरण (a−b)x2+(b−c)x+(c−a)=0 के मूल बराबर हैं तो सिद्ध कीजिए की b+c=2a.
दिया है,
a2b2x2−(4b4−3a4)x−12a2b2=0
अब, दी गई समीकरण की तुलना
Ax2+Bx+c
से करने पर,
A=a2b2,
B=−(4b4−3a4)
=(3a4−4b4)
और C=−12a2b2
∴D=(B2−4AC)
- =(3a4−4b4)2−4a2b2(−12a2b2)
=9a8+16b8−24a4b4+48a4b4
=9a8+16b8+24a4b4
=(3a4)2+(4b4)2+2×3a4×4b4
=(3a4+4b4)2≥0
चूँकि, दी गई समीकरण के मूल वास्तविक हैं।
अतः
α=−B+√D2A
- =(4b4−3a4)+(3a4+4b4)2a2b2
=8b42a2b2
=4b2a2
और
β=−B−√D2A
- =(4b4−3a4)−(3a4+4b4)2a2b2
=−6a42a2b2
=−3a2b2
इसलिए 4b2a2 और −3a2b2 दिए गए समीकरण के अभीष्ट मूल हैं।
सारांस
इस अभ्यास में आपने निम्न तथ्यों का अध्ययन किया है:
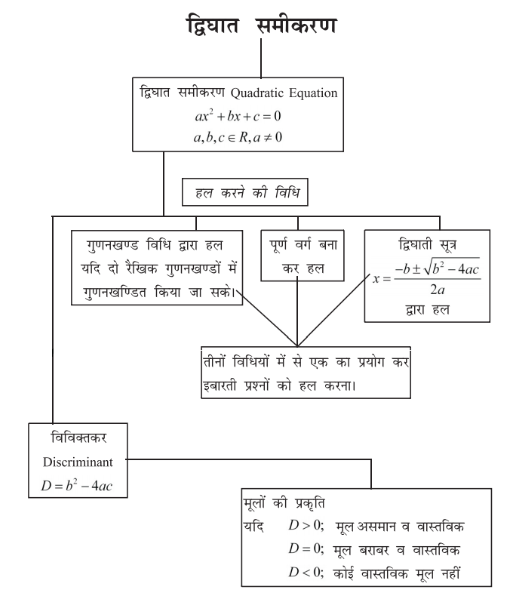
(i) दो भिन्न वास्तविक मूल होते है यदि b2−4ac>0 हो।
(ii) दो बराबर मूल (अर्थात सम्पाती वास्तविक मूल) होते है, यदि b2−4ac=0 हो और
(iii) कोई वास्तविक मूल नहीं होते है, यदि b2−4ac<0 हो।