Complete Solutions to APRIL ATTEMPT (10 APRIL, SHIFT-II) of chapter JEE MAIN 2019 (APRIL & JANUARY ATTEMPT) of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | JEE MAIN 2019 (APRIL & JANUARY ATTEMPT) |
| ARIHANT HINDI | APRIL ATTEMPT (10 APRIL, SHIFT-II) |
| Number Of Questions | 90 |
| Academic Year | 2023-24 |
एक ग्रह की सतह से 20 किमी ऊँचाई पर एक अन्तरिक्षयान ग्रह के परित: कक्षा में घूम रहा है। यदि यान पर सिर्फ ग्रह का गुरुत्वीय क्षेत्र प्रभावी है, तो यान द्वारा 24 घण्टों में लगाए गए पूरे चक्करों की संख्या का मान होगा (दिया है, ग्रह का द्रव्यमान = `8 xx 10^22` किग्रा, ग्रह की त्रिज्या = `2 xx 10^6` मी, गुरुत्वीय नियतांक, `G=6.67 xx 10^(-11) N-m^(2)//kg^(2)`)
View Solutionद्रव्यमान m = 2 के एक कण की स्थिति, समय (t) के अनुसार `r(t) = 2thati -3t^(2) hatj` है। इस कण का मूलबिन्दु के सापेक्ष t = 2 पर कोणीय संवेग होगा-
View Solutionत्रिज्याओं a तथा b (b> a) के दो समकेन्द्रीय चालक गोलों के बीच एक `rho` प्रतिरोधकता का पदार्थ भर दिया जाता है। इन गोलों के बीच प्रतिरोध का मान होगा-
View Solutionयंग के एक द्वि-झिरी प्रयोग में स्लिट की चौड़ाइयों का अनुपात 4:1 है। स्क्रीन पर केन्द्रीय फ्रिज के निकट देखी गई उच्चतम तथा न्यूनतम प्रकाश तीव्रता का अनुपात होगा।
View Solutionसमुद्र में `d_(1)` गहराई पर एक पनडुब्बी `5.05 xx 10^(6) Pa` का दाब अनुभव करती है। जब यह पनडुब्बी और गहराई `d_(2)` पर जाती है, तो `8.08 xx 10^(6)` Pa का दाब अनुभव करती है। तब `d_(2)-d_(1)` का निकटतम मान होगा (दिया है, पानी का घनत्व = `10^(-3)` किग्रा मी-तथा गुरुत्वीय त्वरण = `10 "मी-से"^(2)` )
View Solutionपीतल की प्रत्यास्थता सीमा 379 MPa है। 400 न्यूटन बल को बिना प्रत्यास्थता सीमा पार किए जाने वाली पीतल की छड़ का न्यूनतम व्यास क्या होगा?
View Solutionएक नल से पानी ऊर्ध्वाधर नीचे की ओर 1.0 मी/से की आरम्भिक गति से निकलता है। नल के अनुप्रस्थ-काट का क्षेत्रफल `10^(-4)` मी. है। पानी की धारा में दाब को नियत तथा बहाव को धारारेखीय मानिए। नल से 0.15 मी नीचे धारा का अनुप्रस्थ-काट का क्षेत्रफल होगा (`g = 10 "मी//से^(-2)` लीजिए)।
View Solution0.5 मी भुजा लम्बाई का एक घनाकार गुटका पानी में तैरता है जिससे उसका 30% आयतन पानी में डुबा है। इस गुटके के ऊपर अधिकतम कितना भार, गुटके को बिना पूरी तरह डुबाये रखा जा सकता है? (दिया है, पानी का घनत्व = `10^3 "किग्रा//मी^(3)`)
View Solutionएक सम्पूर्ण अवशोषक पृष्ठ पर 25 वाट `"सेमी"^(-2)` ऊर्जा प्रवाह (flux) का प्रकाश लम्बवत् आपतित होता है। यदि पृष्ठ का क्षेत्रफल `25 "सेमी"^(2)` है, तो 40 मिनट समयान्तराल में उस पर हुआ संवेग अन्तरण (transfer) होगा -
View Solution20 सेमी लम्बाई की मिट्टी की दीवार भेदने से ठीक पहले 20 ग्राम द्रव्यमान की एक गोली की चाल 1 मी/से है। यदि दीवार `25 xx 10^(-2)`N का औसत अवरोध लगाती है, तो दीवार के दूसरे तरफ से निर्गत गोली की चाल का सन्निकट मान होगा
View Solutionएक ध्वनि स्रोत S, 50 मी/से की गति से एक स्थिर श्रोता की तरफ बढ़ रहा है। श्रोता को ध्वनि की आवृत्ति 1000 हर्ट्स सुनाई देती है। जब स्रोत उसी गति से श्रोता को पार करके उससे दूर जाता है, तो श्रोता द्वारा सुनी गई ध्वनि की आवृत्ति का मान होगा (माना वायु में ध्वनि की गति = 350 मी/से)
View Solutionएक 2mW लेजर की तरंगदैर्ध्य 500 nm है। इससे निकलने वाले प्रति सेकण्ड फोटॉनों की संख्या होगी (दिया है, प्लांक नियतांक, `h = 6.6 xx 10^(-34)` Js, प्रकाश की चाल, `c= 3.0 xx 10^(8)` मी/से)
View Solution1 मी भुजा वाले एक समबाहु त्रिभुजाकार वलय में 10 ऐम्पियर धारा प्रवाहित होती है। इसके केन्द्र पर चुम्बकीय क्षेत्र के परिमाण का मान होगा -`(mu_(0) =4pi xx 10^(-7) NA^(-3))` लीजिए|
View SolutionL लम्बाई के एक सरल लोलक को चित्रानुसार एक समान्तर प्लेट संधारित्र के मध्य, जिसमें विद्युत क्षेत्र E है, में रखा है। इसके लोलक का द्रव्यमान m तथा आवेश q है। इस लोलक का आवर्तकाल होगा-
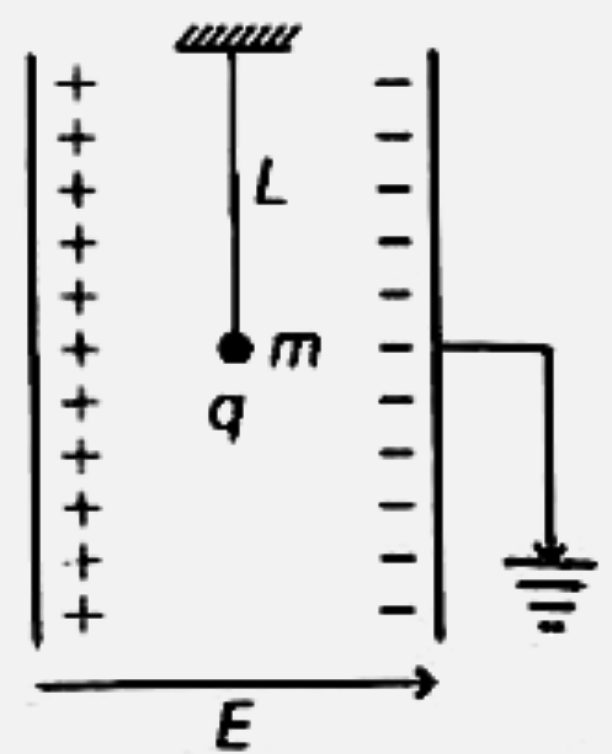
View Solutionसूत्र `x = 5YZ^(2)` में, x तथा Z की विमाएँ क्रमश: धारिता तथा चुम्बकीय क्षेत्र हैं। SI इकाई में Y की विमा क्या होगी?
View Solutionएक वर्गाकार वलय में धारा I प्रवाहित करने पर इसके चुम्बकीय द्विध्रुव आघूर्ण का परिमाण m होता है। यदि इस वर्गाकार वलय को मोड़कर एक वृत्ताकार वलय में परिवर्तित किया जाए और उसमें वही धारा प्रवाहित की जाए, तो इस वृत्ताकार वलय के चुम्बकीय द्विधुव आघूर्ण का परिमाण होगा -
View Solution`Li^(++)` आयन में इलेक्ट्रॉन को उसकी प्रथम बोहर कक्षा से `lambda` तरंगदैर्ध्य के विकिरण से एक ऊँची कक्षा में उत्तेजित कर जाता है। जब यह आयन अपनी न्यूनतम ऊर्जा अवस्था में सभी सम्भव तरीकों (मध्यवर्ती उत्सर्जनों को मिलाकर) से आए, तो कुल 6 स्पेक्ट्रम लाइनें पाई जाती हैं। `lambda` का मान क्या होगा? (दिया है- `h=6.63 xx 10^(-24) Js, c= 3 xx 10^(8) ms^(-1)`)
View Solution11 Hz तथा 9 Hz आवृत्ति की दो तरंगों के अध्यारोपण को निम्न में कौन-सा चित्र योजनाबद्ध तरीके से सही दर्शाता है?
View Solutionद्रव्यमान `m_(A) =1 kg` तथा `m_(B)= 3 kg` के दो गुटकों A तथा B को चित्रानुसार एक मेज पर रखा गया है। A तथा B के बीच घर्षण गुणांक 0.2 एवं B तथा मेज के बीच भी घर्षण गुणांक 0.2 है। गुटके B पर लगाए गए क्षैतिज बल F का अधिकतम मान, जिससे गुटका A, गुटका B के ऊपर नहीं फिसले, होगा (दिया है, `g= 10 m//s^(2)`)
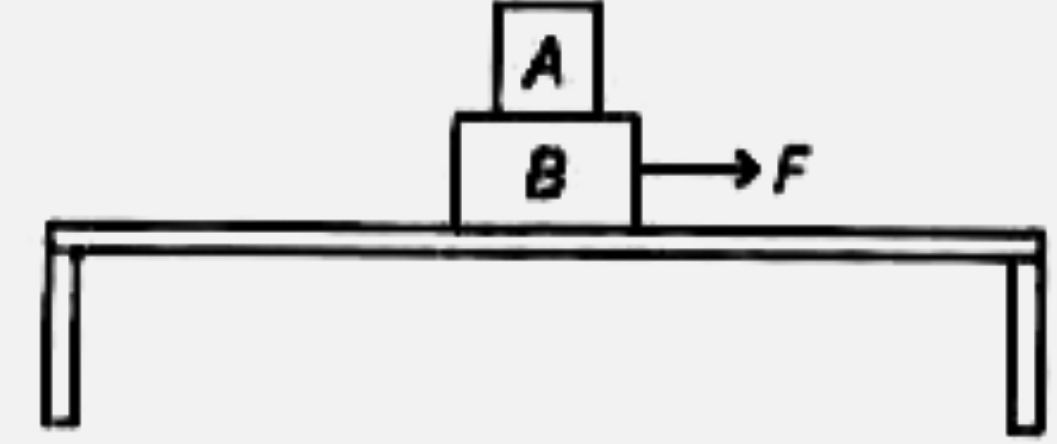
View Solutionद्रव्यमान M तथा त्रिज्या R के एक ठोस गोले को दो असमान हिस्सों में बाँटा जाता है।`(7M)/8` द्रव्यमान के पहले हिस्से को एक 2R त्रिज्या की एकसमान डिस्क में बदला जाता है। बचे हुए हिस्से से एक एकसमान ठोस गोला बनाया जाता है। मानाकि `I_(1)` डिस्क का उसकी अक्ष के परितः जड़त्व आघूर्ण है तथा `I_(2)` नये गोले का उसके अक्ष के परितः जड़त्व आघूर्ण है। अनुपात `I_(1) I_(2)` होगा-
View Solutionदिए गए ग्राफ में एक पतले लेन्स के आवर्धन m को प्रतिबिम्ब की दूरी v के साथ दर्शाता है। इस लेन्स की फोकस दूरी क्या होगी?
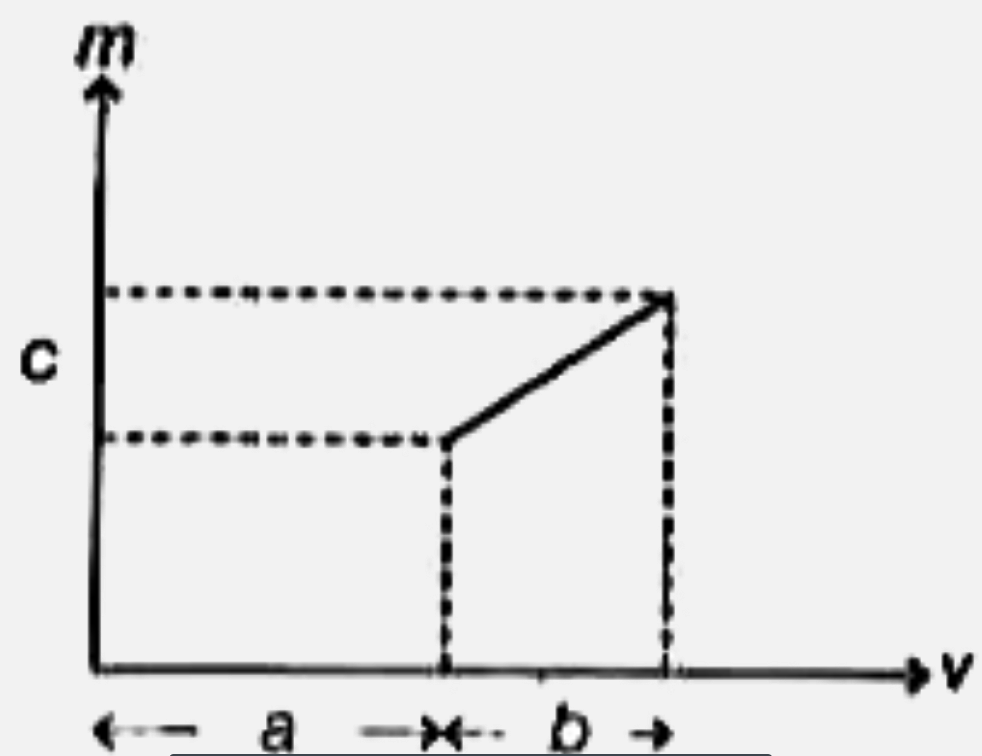
View Solutionदो रेडियोधर्मी पदार्थों A तथा B के क्षय नियतांक क्रमश: `5 lambda` तथा `lambda` हैं। t = 0 पर एक नमूने में इन दो नाभिकों की बराबर संख्या है। नाभिकों की संख्या का अनुपात `(1/e)^(2)` होने में लगे समय का मान होगा-
View Solutionएक आदर्श गैस का एक मोल ऐसे प्रक्रम से गुजरता है, जिसमें दाब तथा आयतन सूत्र `p=p_(0)[1-1/2 (V_(0)/V)^(2)]` से सम्बन्धित हैं। यहाँ, `p_(0)` तथा `V_(0)` नियतांक हैं। यदि गैस का आयतन `V_(0)` से बढ़कर 2`2 V_(0)` होता है, तो इसके तापमान का बदलाव होगा
View Solution10 mH स्वप्रेरकत्व एवं `0.1 Omega` प्रतिरोध की एक कण्डली को एक कँजी के साथ एक `0.90 Omega` आन्तरिक प्रतिरोध के सेल से जोड़ते हैं। कुंजी को बन्द करने के पश्चात् इस परिपथ में धारा का मान संतृप्त धारा के 80% होने में लगा समय होगा (दिया है, ln = 1.6)
View Solutionएक समतल क्षैतिज से `alpha` = 30° का कोण बनता है। एक कण को इस समतल के आधार से गति `u=2ms^(-1)` से समतल से `theta = 15^(@)` के कोण पर चित्रानुसार प्रक्षेपित किया जाता है। उस बिन्दु, जहाँ कण समतल पर गिरता है, की आधार से दूरी का सन्निकट मान होगा (`g = 10 ms^(-1)` लीजिए)
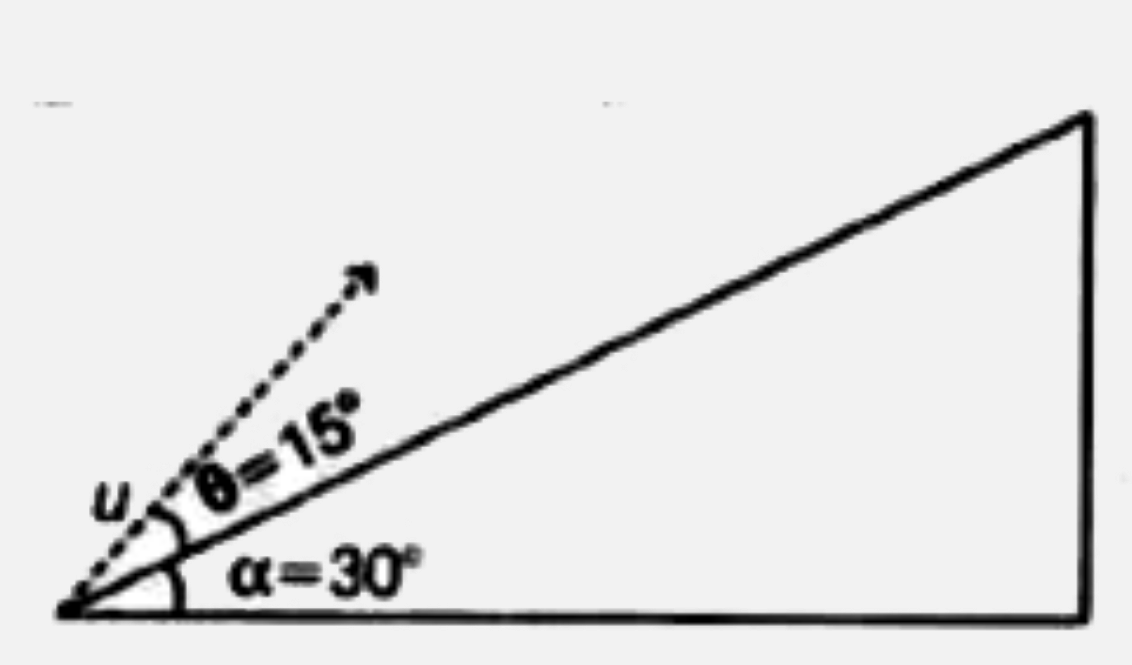
View Solutionएक प्रयोग में पीतल तथा स्टील के दो तारों का प्रयोग किया गया है, जिनमें प्रत्येक की लम्बाई 1 m तथा अनुप्रस्थ-काट का क्षेत्रफल 1 mm है। इन तारों को श्रेणीक्रम में जोड़ते हैं तथा संयुक्त तार के एक सिरे को दृढ़ स्तम्भ से जोड़ते हैं एवं दूसरे सिरे को खींचा जाता है। 0.2 mm की कुल वृद्धि के लिए प्रतिबल का मान होगा (दिया है स्टील तथा पीतल के यंग प्रत्यास्थता गुणांक, `120 xx 10^(9) N//m^(2)` तथा `60 xx 10^(9) N//m^(2)`)
View Solutionनिर्वात में एक `1 muC` आवेश के एक कण A को बिन्दु P पर दृढ़ रखा है। उसी आवेश तथा `4mug` द्रव्यमान के दूसरे कण B को P से 1mm दूरी पर रखा है। B को छोड़ने पर P से 9 mm दूरी पर उसकी गति का मान होगा (दिया है, `1/(4pi epsilon_(0)) = 9 xx 10^(9) N-m^(2) C^(-2)`)
View Solutionदृढ़ अणुओं वाली एक द्विपरमाणुक गैस को जब Q ऊष्मा नियत आयतन पर दी जाती है, तो उसके तापमान में `DeltaT` की वृद्धि होती है। इसी तापमान वृद्धि को नियत दाब पर सुनिश्चित करने के लिए आवश्यक ऊष्मा होगी-
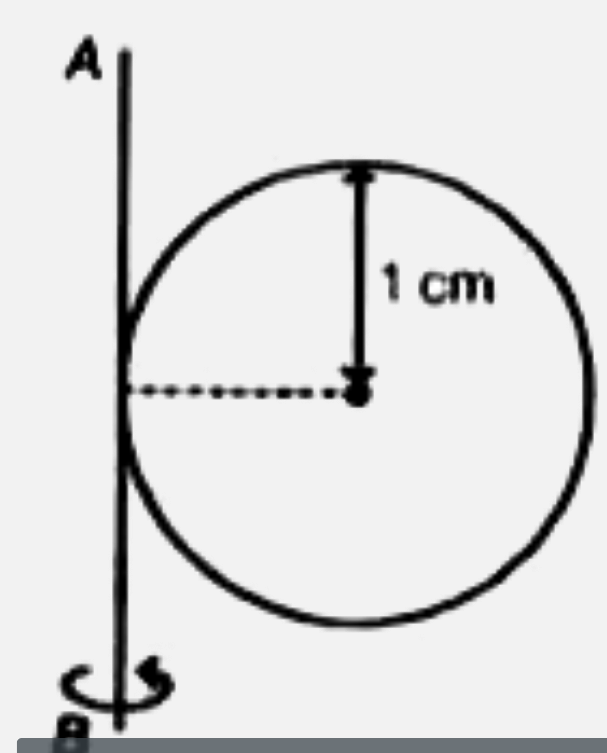
View Solution5g द्रव्यमान तथा 1 cm त्रिज्या के धातु के एक सिक्के को एक पतली नगण्य द्रव्यमान की छड़ AB से चित्रानुसार जोड़ा गया है। यदि निकाय आरम्भ में स्थिरावस्था में है, तो इसे AB के परितः 58 तक 25 चक्कर प्रति सेकण्ड की गति से घुमाने के लिए नियत बल-आघूर्ण का सन्निकट मान होगा|
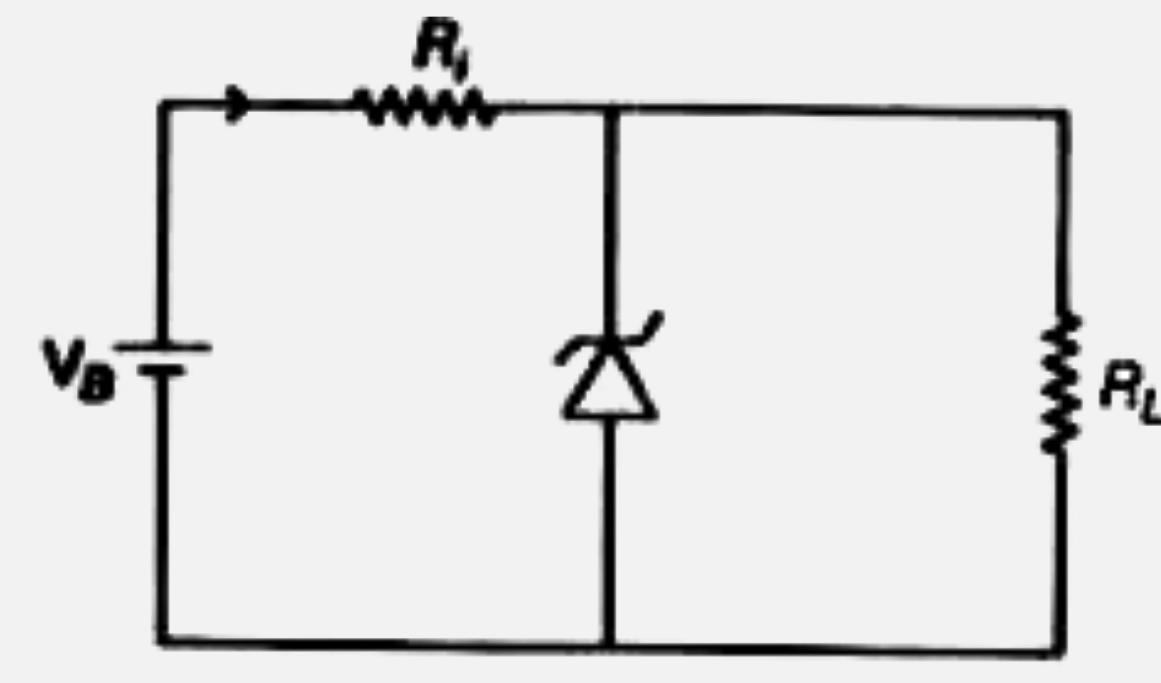
View Solutionचित्र में जेनर डायोड से बनाया हुआ वोल्टेज नियन्त्रण परिपथ दिखाया गया है। जेनर डायोड की भंजन वोल्टता 6V तथा लोड प्रतिरोध `R_(L)=4 k Omega` है, श्रेणी प्रतिरोध `R_(i) = 1 kOmega` है। यदि सेल का विभव `V_B, 8 V` से 16V के बीच बदलता है, तो जेनर डायोड की धारा के न्यूनतम तथा अधिकतम मान क्या होंगे?
View Solutionएक व्यक्ति (द्रव्यमान = 50 kg) तथा उसका बेटा (द्रव्यमान = 20 kg) किसी घर्षणरहित पृष्ठ पर एक-दूसरे के सामने खड़े हैं। वह व्यक्ति अपने बेटे को धकेलता है। जिससे वह उस व्यक्ति के सापेक्ष `0.70 ms^(-1)` की चाल से गति करने लगता है, तो उस व्यक्ति की पृष्ठ के सापेक्ष चाल होगी-
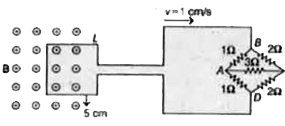
View Solutionयहाँ आरेख में 5 cm भुजा का एक वर्गाकार पाश L दर्शाया गया है, जो प्रतिरोधों के एक परिपथ से है। यह संयोजन 1 cm `s^(-1)` की एकसमान चाल से दाईं ओर गति कर रहा है। किसी क्षण L का एक भाग 1 T तीव्रता के एकसमान चुम्बकीय क्षेत्र में है। यह क्षेत्र पाश L के समतल के लम्बवत् है। यदि इस पाश का प्रतिरोध 1.7 `Omega` है, तो इस क्षण इसमें धारा का निकट मान होगा
View Solutionकिसी स्थिर तोप से एक गोला प्रारम्भिक चाल - से ऐसे कोण पर दागा जाता है कि गोलका भूतल पर अपने लक्ष्य पर लगता है, लक्ष्य की तोप से दूरी R है। यदि गोले द्वारा लक्ष्य पर लगने के दो सम्भव मार्ग हैं और इनमें लगे समय क्रमश: `t_(1)` तथा `t_2` हैं, तो गुणनफल `t_(1)t_(2)` होगा-
View Solution`-10°`C तापमान के `M_(1)` ग्राम बर्फ (विशिष्ट ऊष्मा =`0.5 cal g^(-1) C^(-1)` को, 50°C तापमान के M, ग्राम जल में डालने पर पूरी बर्फ पिघल जाती है और जल का तापमान 0°C हो जाता है, तो बर्फ की गुप्त ऊष्मा का मान (`cal g^(-1)` में)
View Solutionl लम्बाई की किसी एकसमान छड़ को क्षतिज समतल में एक स्थिर कोणीय चाल से घुमाया जा रहा है। घूर्णन-अक्ष छड़ के एक सिरे से गुजरती है। यदि इस घूर्णन के कारण छड़ में उत्पन्न तनाव अक्ष से x दूरी पर T (x) है, तो निम्नांकित में से कौन-सा ग्राफ इसे सर्वाधिक निकट रूप से दर्शाता है?
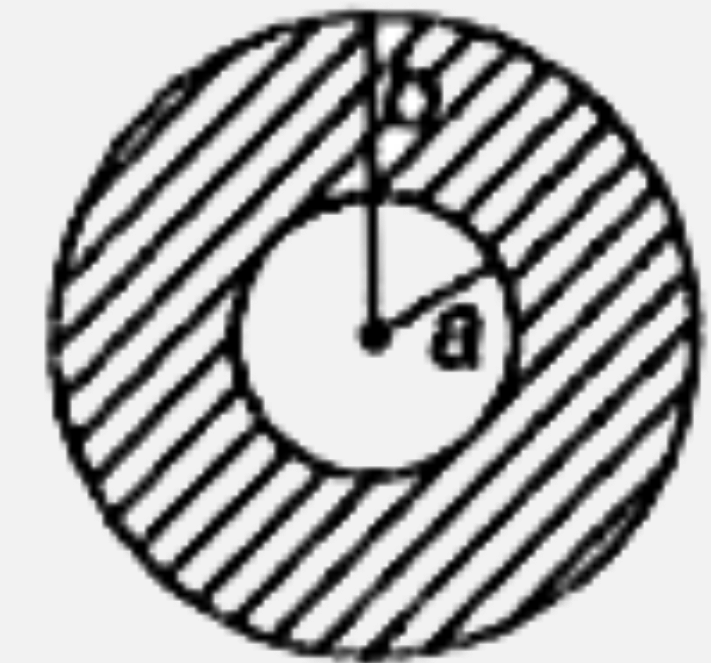
View Solutionकिसी वृत्ताकार डिस्क की त्रिज्या b है। इसमें एक छिद्र इसके केन्द्र पर बना है, जिसकी त्रिज्या a है। यदि डिस्क के प्रति एकांक क्षेत्रफल का द्रव्यमान,`(sigma_(0)/r)` के अनुसार परिवर्तित होता है, तो इसके केन्द्र से गुजरने वाली अक्ष के परित: डिस्क की परिभ्रमण त्रिज्या होगी-
View Solutionदिए गए परिपथ के लिए सत्यमान सारणी है-
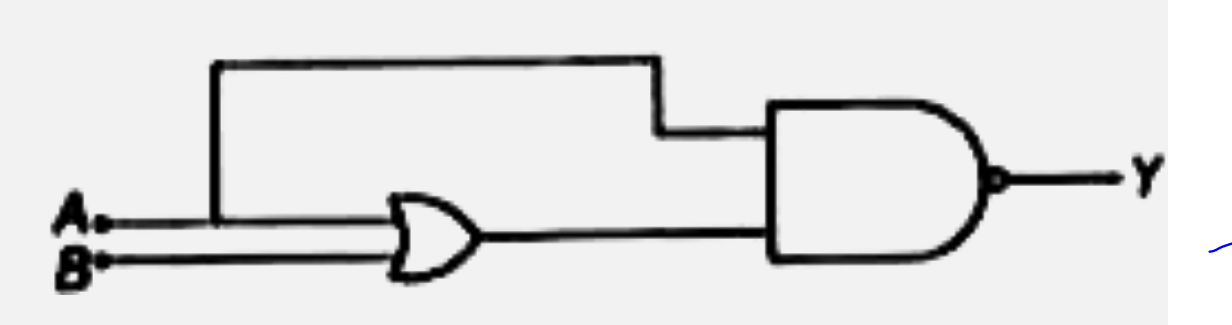
View Solutionनिम्नांकित में से किस संयोजन की विमा वही है, जो विद्युत प्रतिरोध की है (यहाँ, `epsilon_(0)` निर्वात की विद्युतशीलता (परावैधुतांक) तथा `mu_(0)` निर्वात की चुम्बकशीलता है)?
View Solutionकिसी धारामापी का प्रतिरोध 1000 है। इसके स्केल पर 50 भाग है और इसकी सुग्राहिता `20 muA` भाग है। इसे एक ऐसे वोल्टमीटर में परिवर्तित करना है, जिसकी तीन परास `0.2V, 0-10 V` तथा 0-20V हैं। इसके लिए लगभग उपयुक्त परिपथ होगा-
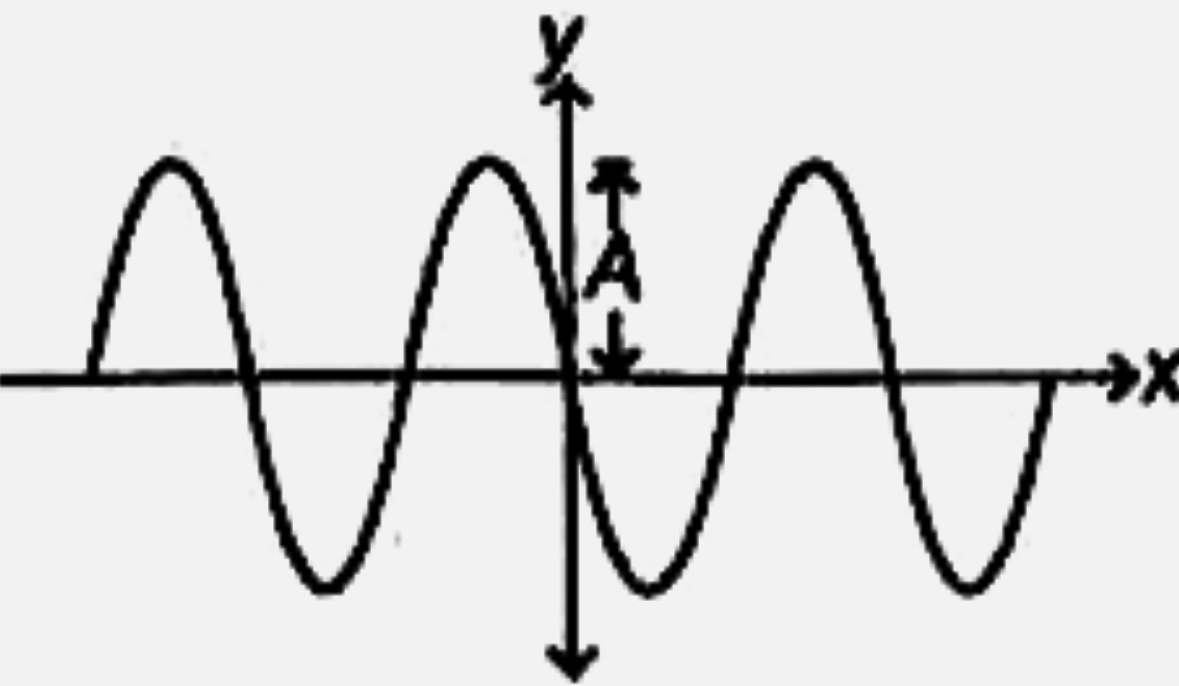
View Solutionधनात्मक दिशा में गमन करती हुई किसी प्रगामी तरंग को `y(x,t) =A sin(kx - omegat + phi)` से निरूपित किया जाता है। t=0 पर खींचा गया आशु चित्र निम्न से दिया जाता है इस तरंग के लिए कला `phi` का मान होगा-
View Solutionओम के नियम का सत्यापन करने के लिए एक छात्रा वोल्टमीटर को एक बैटरी के सिरों के बीच जोड़ती है और परिपथ में वोल्टता (V) तथा विद्युत धारा (L) के विभिन्न मान प्राप्त कर, निम्नांकित ग्राफ बनाती है।
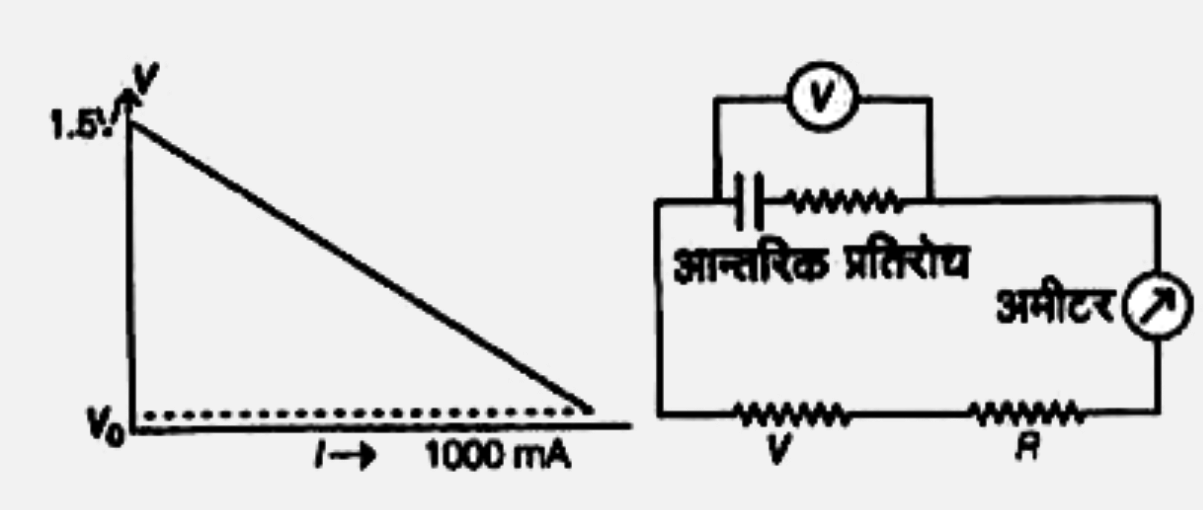
यदि `V_(0)` का मान लगभग शून्य है, तो सही कथन का चयन कीजिए।
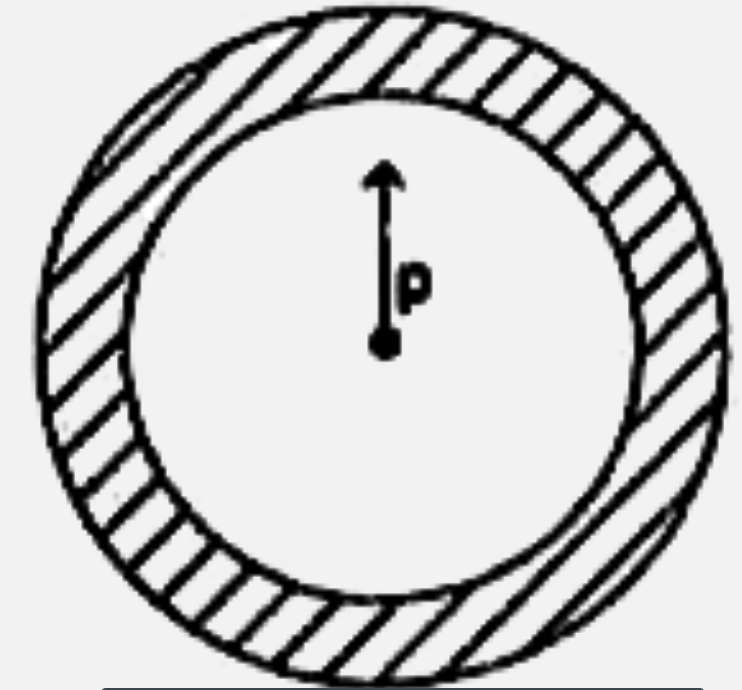
View Solutionयहाँ आरेख में एक चालक-कोश (शैल) को दर्शाया गया है। इसकी आन्तरिक व बाह्य त्रिज्यायें क्रमश: a तथा b हैं, इस कोश पर आवेश है, इसके केन्द्र पर एक द्विध्रुव है (आरेख देखिए)। इस स्थिति में-
View Solution18 km/h की चाल से गतिशील एक पनडुब्बी (A) का पीछा उसकी गति के अनुसार 27 km/h की चाल से गतिशील दूसरी पनडुब्बी (B) करती है। A को खोजने के लिए B,500 Hz का एक ध्वनिक सिग्नल भेजती है, तो आवृत्ति v की परावर्तित ध्वनि प्राप्त होती है। v का मान लगभग होगा (पानी में ध्वनि की चाल- `1500 ms^(-1)`)
View Solution40°C तापमान पर 1mm त्रिज्या का पीतल का एक तार छत से लटकाया गया है। तार के मुक्त सिरे से M द्रव्यमान के एक छोटे पिण्ड को लटकाया गया है। जब तार को 40°C से 20°C पर ठण्डा करते हैं, तो वह वापस अपनी पुरानी लम्बाई 0.2 m को प्राप्त कर लेता है। M का निकटतम मान होगा (पीतल का रेखीय प्रसार गुणांक तथा यंग प्रत्यास्थ गुणांक क्रमशः हैं `10^(-5) l^(@)C` तथा `10^(11) N//m^(2)` एवं `g=10 ms^(-2)`)
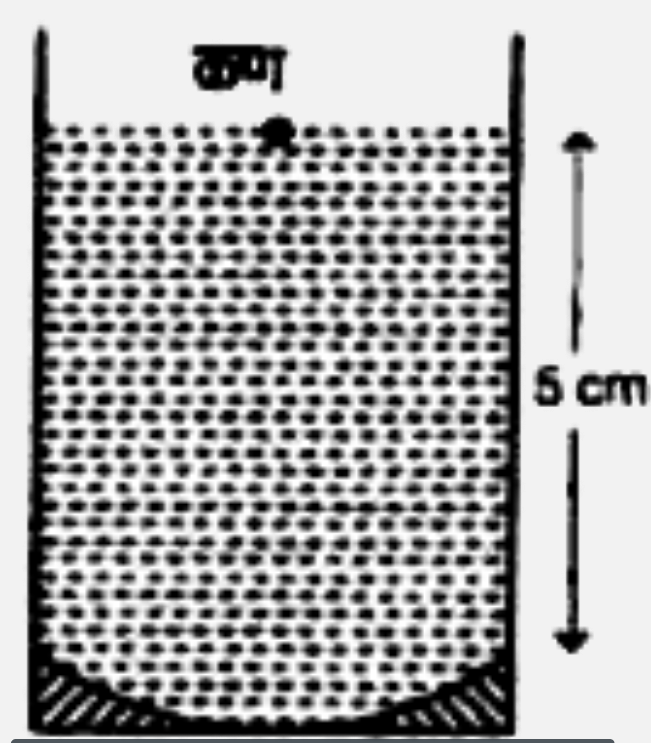
View Solution40 cm वक्रता त्रिज्या कण का एक अवतल दर्पण, आरेख (चित्र) में दर्शाए गए अनुसार, एक गिलास की तली में रखा 5 cm है। गिलास में 5 cm ऊँचाई तक जल भरा है। एक छोटा सा कण जल की सतह पर तैर रहा है। गिलास के ठीक ऊपर से देखने पर इसका प्रतिबिम्ब जल की सतह से d दूरी पर है, तो d का निकट मान होगा (पानी का अपवर्तनांक 1.33)
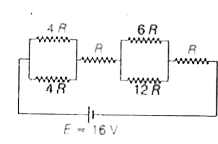
View Solutionदर्शाए गए प्रतिरोधकों के परिपथ को 16V के एक DC स्रोत से जोड़ा गया है। परिपथ द्वारा उपभुक्त शक्ति 4 वाट है, तो R का मान होगा
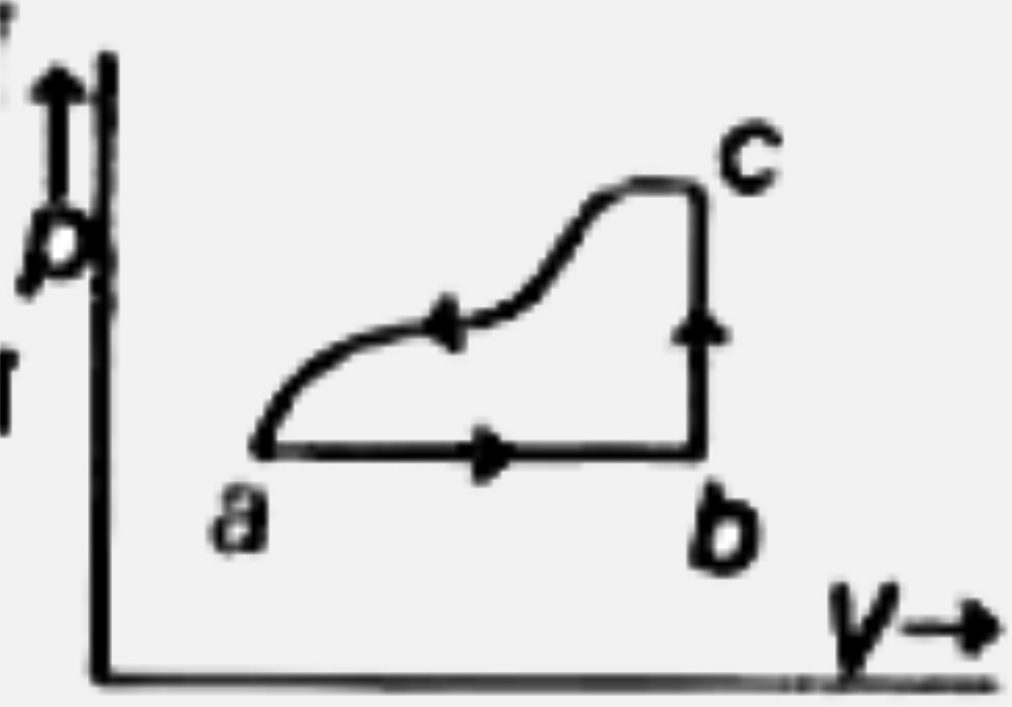
View Solutionएक आदर्श गैस को चित्र में। दर्शाए गए अनुसार चक्रीय प्रक्रम abea से गुजारा जाता है। ca पथ के अनुदिश गैस a की आन्तरिक ऊर्जा में। परिवर्तन - 180J है। ab पथ के अनुदिश 250 J ऊष्मा अवशोषित करती है तथा bc पथ के अनुदिश गैस 60 J ऊष्मा अवशोषित करती है, तो पथ abc के अनुदिश गैस द्वारा किया गया कार्य है-
View Solutionएक सूक्ष्मदर्शी के अभिदृश्यक लेन्स की संख्यात्मक द्वारक (numerical aperture) का मान 1.25 है। यदि 5000 A तरंगदैर्ध्य का प्रकाश प्रयोग करें, तो दो बिन्दुओं को अलग-अलग देखने के लिए उनके बीच की न्यूनतम दूरी होगी-
View Solutionएक विद्युत चुम्बकीय तरंग को विद्युत क्षेत्र `E=E_(0)hatn sin[omegat + (6y -8z)]` से निरूपित किया जाता है। यदि x,y तथा z-दिशा में इकाई सदिश क्रमश: `hati, hatj` तथा `hatk` हैं, तो संचरण की दिशा के लिए सही विकल्प है-
View Solutionकिसी प्रक्षेप्य के प्रक्षेप्य-पथ को भू-पृष्ठ पर `y=2x - 9x^(2)` से निरूपित किया जाता है। यदि इसे `v_(0)` चाल द्वारा `theta_(0)` कोण पर प्रमोचित किया गया होता, तो- `(g=10 ms^(-2))`
View Solutionएक द्वि-झिरी प्रयोग में किसी एक झिरी के सामने t मोटाई तथा `mu` अपवर्तनांक की एक पतली फिल्म रख देने से फ्रिज पैटर्न का केन्द्रीय उच्चिष्ठ एक फ्रिज की चौड़ाई के बराबर विस्थापित हो जाता है, तो t का मान है (`lambda` प्रकाश की तरंगदैर्ध्य है)
View Solutionएक बिन्दु द्विध्रुव `p =-p_(0) hatx` मूलबिन्दु पर स्थित है, तो इस द्विध्रुव के कारण Y. अक्ष पर d दूरी पर विभव तथा विद्युत क्षेत्र क्रमशः होंगे (माना अनन्त पर V = 0 है)
View Solutionएक व्यक्ति (द्रव्यमान = M) L लम्बाई के एक झुले पर झूल रहा है। झूले का कोणीय आयाम , है। झूले के अपने निम्नतम बिन्दु से गुजरते समय वह व्यक्ति झूले पर खड़ा हो जाता है। यदि खड़े होने से उस व्यक्ति का द्रव्यमान केन्द्र `l( l lt lt L)` दूरी से विस्थापित हो जाता है, तो व्यक्ति द्वारा किया गया कार्य होगा।
View Solution10 cm त्रिज्या की एक रिंग पर आवेश एकसमान रूप से वितरित है। यह रिंग `40 pi rad s^(-1)` की एकसमान दर से अपने अक्ष के परितः घूर्णन कर रही है तथा आवेश रिंग के समतल के लम्बवत् है। यदि इसके केन्द्र पर चुम्बकीय क्षेत्र `3.8 xx 10^(-9)` T है, तो रिंग पर आवेश लगभग होगा- `(mu_(0) = 4pi xx 10^(-7) N//A^(2))`
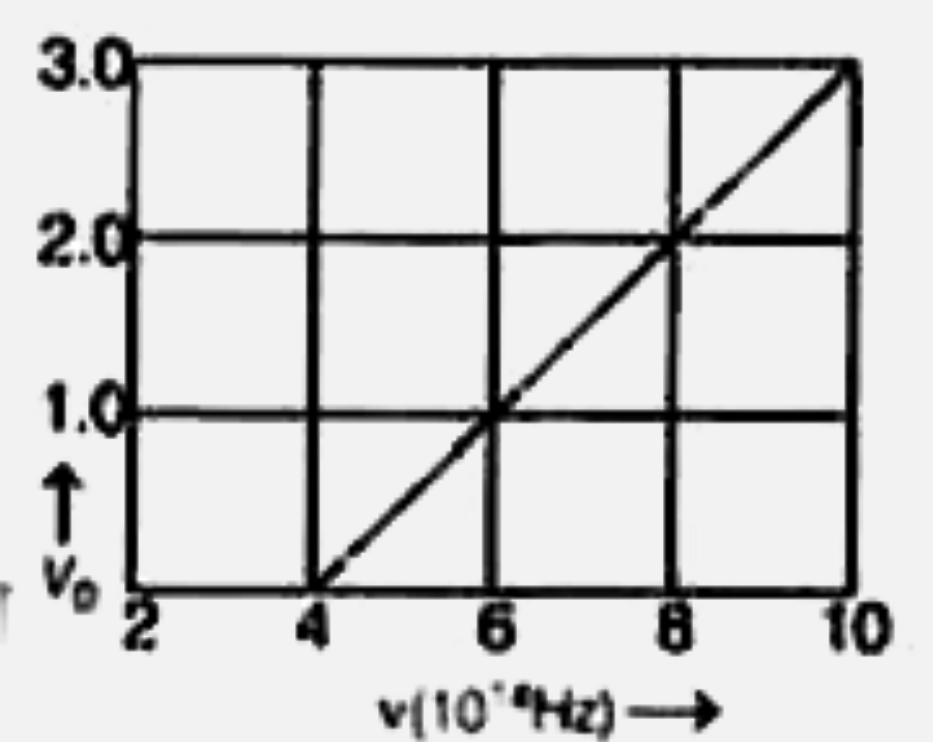
View Solutionयहाँ आरेख में एक 30 सोडियम-उत्सर्जक के ( v) लिए आवृत्ति (v) के 24 फलन के रूप में निरोधी विभव `V_(0)` (वोल्ट में) के परिवर्तन को दर्शाया गया है। इस v ग्राफ से सोडियम का कार्य-फलन प्राप्त होगा (प्लांक स्थिरांक, `h= 6.63 xx 10^(-34) Js`, इलेक्ट्रॉन आवेश, `e=1.6 xx 10^(-19) C`)
View Solutionहीलियम गैस के दो मोल को हाइड्रोजन के तीन मोल अणुओं (जोकि दृढ़ माने गए हैं) के साथ मिलाया जाता है। स्थिर आयतन पर इस मिश्रण की मोलर विशिष्ट ऊष्मा क्या होगी? `(R= 8.3 J//mol-K)`
View Solutionदो सर्वसम समान्तर पट्टिका संधारित्रों में प्रत्येक की धारिता C है, उनकी प्लेटों (पट्टिकाओं) का क्षेत्रफल A है और पट्टिकाओं के बीच की दूरी d है। दोनों प्लेटों के बीच के स्थान को `K_(1), K_(2)` तथा `K_(3)` परावैद्युतांक के तीन परावैद्युत स्लैब से भर दिया है, सभी स्लैबों की मोटाई समान है। किन्तु पहले संधारित्र में उन्हें आरेख I के अनुसार तथा दूसरे में आरेख II के अनुसार रखा गया है (`E_(1)` तथा `E_(2)` क्रमश: प्रथम तथा द्वितीय संधारित्र से सम्बन्धित हैं)। यदि इन नए संधारित्रों में प्रत्येक को समान विभव V से आवेशित किया जाए, तो उनमें संचित ऊजाओं का अनुपात होगा-
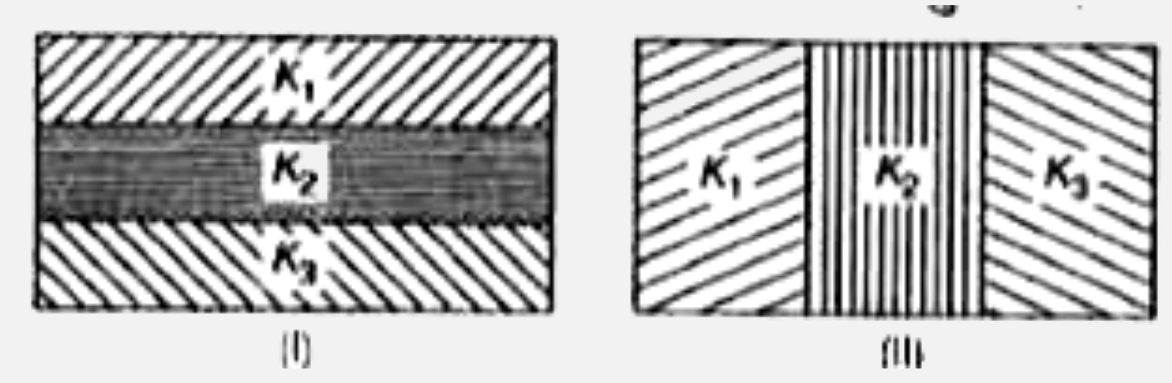
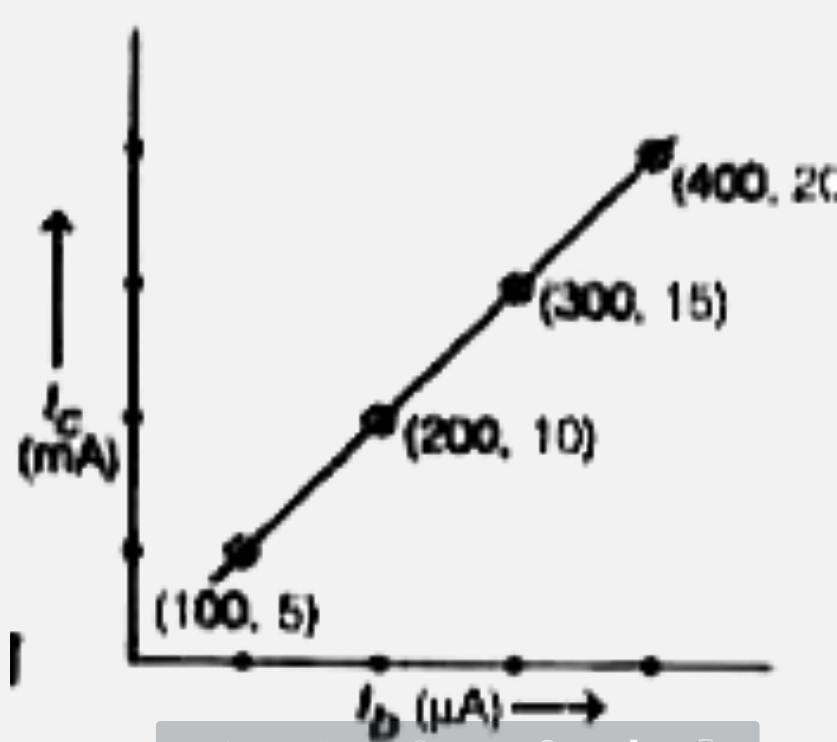
View Solutionकिसी ट्रांजिस्टर के निवेश तथा निर्गम प्रतिरोध क्रमश: `100 Omega` तथा `100 kOmega` हैं। इसके लिए अन्तरण अभिलक्षण वक्र यहाँ दर्शाया गया है, तो वोल्टता तथा शक्ति लब्धि क्रमश: हैं-
View Solutionदो स्थानों पर नमन कोणों का मान क्रमश: 45° तथा 30° है। इन स्थानों पर एक चुम्बकीय सुई एक मिनट में क्रमश: 30 तथा 40 दोलन करती है। यदि इन दो स्थानों पर पृथ्वी के कुल चुम्बकीय क्षेत्र की तीव्रता क्रमशः `B_(1)` तथा `B_(2)` है, तो अनुपात `B_(1)//B_(2)` का निकटतम मान होगा-
View Solutionएक उत्तेजित `He^+` आयन अपनी न्यूनतम ऊर्जा अवस्था में संक्रमण होने तक दो क्रमागत फोटॉन, जिनकी तरंगैदy 108.5 nm तथा 30.4 nm हैं, उत्सर्जित करता है। प्रारम्भिक उत्तेजित अवस्था के संगत क्वाण्टम संख्या n है ( `lambda` तरंगदैर्ध्य के लिए फोटॉन की ऊर्जा =`(1240 eV)/(lambda(nm में))`
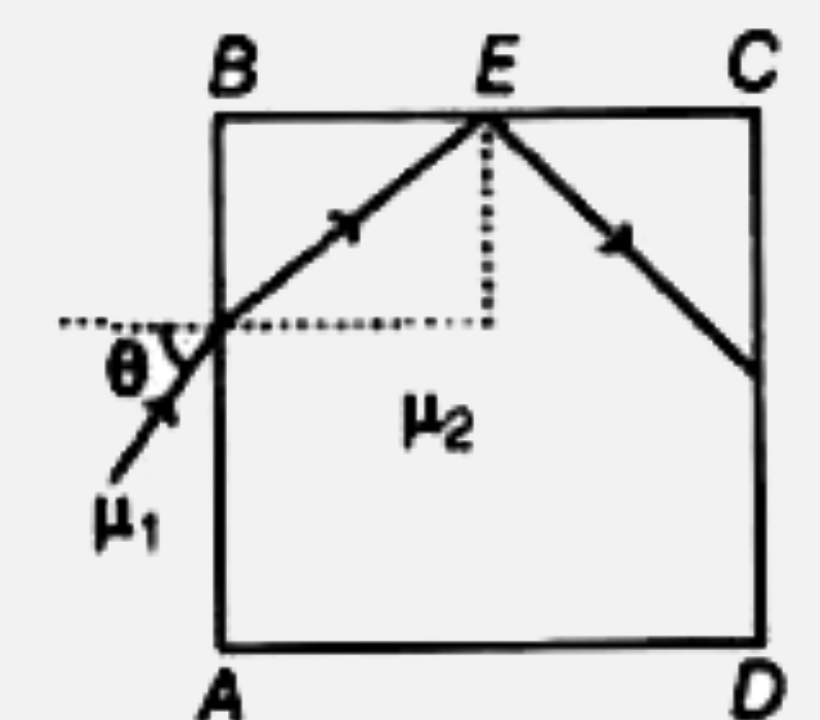
View Solutionअपवर्तनांक `mu_(1)` के एक द्रव में अपवर्तनांक `mu_(2)(mu_(1) lt mu_(2))` के पारदर्शी गुटके को डुबोया जाता है। प्रकाश की एक किरण इस गुटके के पृष्ठ AB पर द्रव से चित्रानुसार कोण पर आपतित होती है। पृष्ठ BC के बिन्दु E पर पूर्ण आन्तरिक परावर्तन होने के लिए, `theta` का मान कौन-सा सम्बन्ध सन्तुष्ट करेगा?
View Solutionएक स्प्रिंग की स्वतन्त्र लम्बाई l तथा बल नियतांका है। इसे काटकर `l_(1)` तथा `l_(2)` स्वतन्त्र लम्बाई की दो स्प्रिंगों में बाँटते हैं। `l_(1) = nl_(2)` है, जहाँ n एक पूर्णांक है। इनसे सम्बद्ध बल नियतांकों `k_(1)` तथा `k_(2)` का अनुपात `k_(1)/k_(2)` होगा |
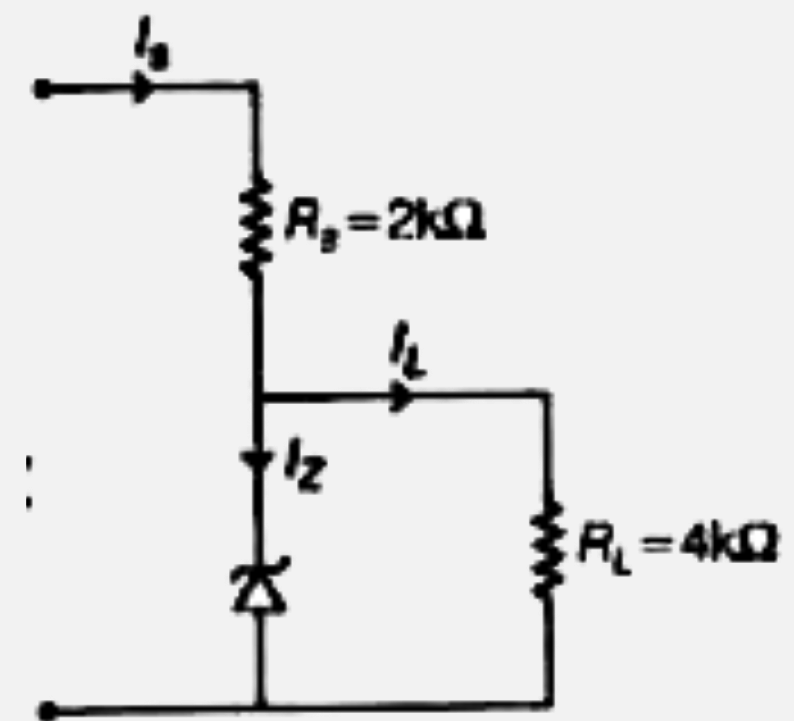
View Solutionचित्र में भंजन वोल्टता = 6 वोल्ट के जेनर डायोड से बनाया विद्युत नियन्त्रक परिपथ दिखाया गया है। यदि अनियन्त्रित निवेशित विभव 10 वोल्ट तथा 16 वोल्ट के बीच बदलता है, तो जेनर डायोड में अधिकतम धारा का मान होगा|
View Solutionदो कणों को एक ही बिन्दु से एक ही चाल u से प्रक्षेपित किया जाता है जिससे उनकी परास R बराबर हैं किन्तु अधिकतम ऊँचाइयाँ `h_(1)` तथा `h_(2)` भिन्न हैं। निम्न में से सत्य कथन चुनिए।
View Solutionएक गैस के अणुओं की संख्या घनत्व मूलबिन्दु से दूरी पर निम्न ढंग से निर्भर है `n^( r) = n_(0)e^(-ar^(4))` , तो इस गैस के अणुओं की कुल संख्या किसके समानुपाती होगी?
View Solutionएक दृढ़ अणुओं वाली द्विपरमाणुक गैस का जब नियत दाब पर प्रसार होता है, तो 10 जूल कार्य करती है। इस प्रक्रम में गैस द्वारा अवशोषित ऊष्मा का मान होगा |
View Solutionकुल आवेश 2Q को त्रिज्या R के गोले में इस प्रकार वितरित करते हैं कि आवेश घनत्व सम्बन्ध p(r) = kr से दिया जाता है, जहाँ । केन्द्र से दूरी है। दो बराबर -Q आवेशों A तथा B को केन्द्र से दूरी पर व्यासीय विपरीत बिन्दुओं पर रखा गया है। यदि A और B कोई बल अनुभव नहीं करते हैं, तो
View Solutionएक कण चाल `v=bsqrt(x)` से धनात्मक X-अक्ष की दिशा में चल रहा है। समय `t = tau` पर कण की चाल होगी (माना कि t = 0 पर कण मूलबिन्दु पर है)
View Solutionएक हाइड्रोजन परमाणु में इलेक्ट्रॉन पहले तीसरी उत्तेजित अवस्था से दूसरी उत्तेजित अवस्था में और तत्पश्चात् दूसरी से प्रथम उत्तेजित अवस्था में जाता है। इन दो संक्रमणों में उत्सर्जित फोटॉनों के संगत तरंगदैर्यों का अनुपात `lambda_(1)//lambda_(2)` होगा |
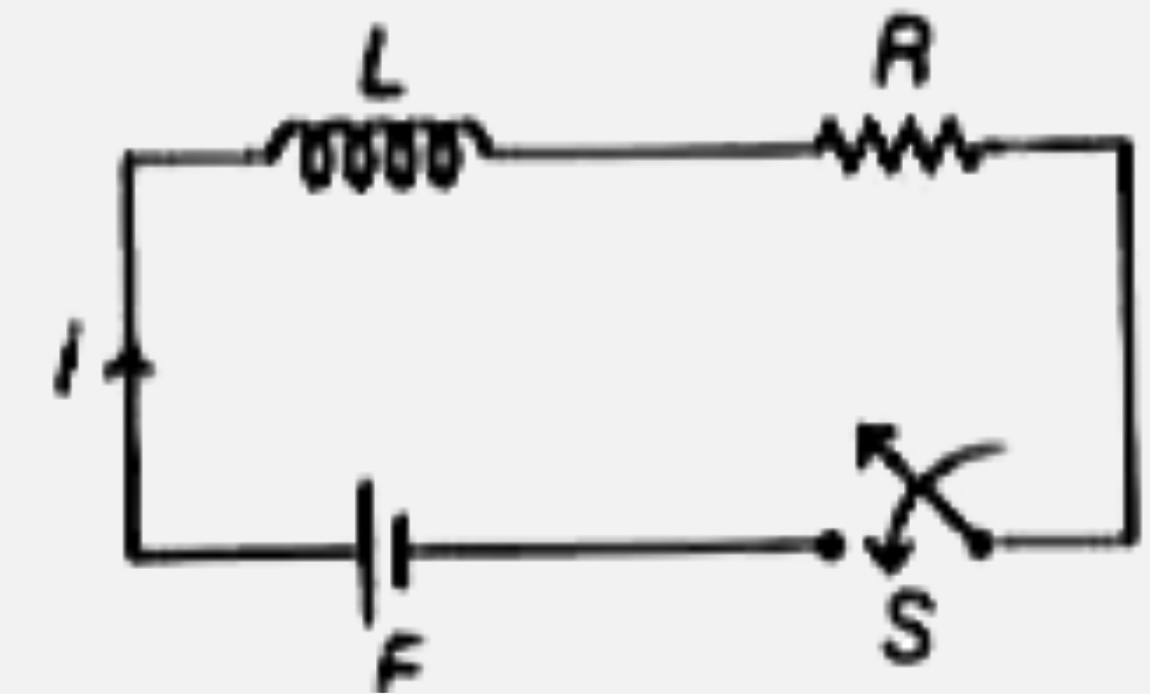
View Solutionचित्र में एक L-R परिपथ दर्शाया है। यदि t = 0 पर कुंजी S को बन्द करते E हैं, तो सेल से निकलने वाले आवेश का मान समयान्तराल t = 0 से `t=L/R` के बीच होगा-
View Solutionअनुनाद नली विधि द्वारा वायु में ध्वनि की चाल (v) ज्ञात करने के लिए एक प्रयोग में 480 Hz आवृत्ति के स्वरिन का उपयोग करते हैं। वायु स्तम्भ की दो उत्तरोत्तर लम्बाइयों `l_(1) = 30` सेमी तथा `l_(2) = 70` सेमी के लिए अनुनाद प्राप्त होते हैं, तब v का मान है-
View Solutionलम्बाई L तथा त्रिज्या 7 की एक एकसमान बेलनाकार छड़ का यंग प्रत्यास्थता गुणांक Y है। जब इस छड़ का तापमान T से बढ़ाते हैं तथा । उस पर कुल अनुदैर्ध्य सम्पीडन बल F लगाते हैं, तो उसकी लम्बाई अपरिवर्तित रहती है। छड़ के पदार्थ के आयतन प्रसार गुणांक का लगभग मान होगा-
View Solutionमाध्य प्रतिरोध (तापमान औसत) 202 की एक विद्युत केतली में 20°C के 1 किग्रा पानी को उबालते हैं। विद्युत आपूर्ति की rms वोल्टता 200 वोल्ट है। केतली से ऊष्मा हानि को नगण्य मानते हुए पानी को पूर्णतया वाष्पित होने में लगभग समय लगेगा [पानी की विशिष्ट ऊष्मा = `4200 J//(kg^(@)C)` , पानी की गुप्त ऊष्मा =2260 kJ/kg)
View Solutionत्रिज्या R के एक ठोस गोले का श्यानता गुणांक `eta` के एक द्रव में (गुरुत्वीय बल के कारण) सीमान्त वेग `v_(1)` है। यदि इस ठोस गोले को बराबर त्रिज्या के 27 गोलों में बाँटा जाए, तो प्रत्येक गोले का सीमान्त वेग इसी द्रव में पाया जाता है, तो `v_(2)` का मान होगा-
View Solutionएक आयामी मॉडुलन परिपथ में निवेशी वाहक तरंग `C(t) = 4 sin(20000 pi t)` है, जबकि मॉडुलन सिग्नल `m(t) = 2 sin (2000 pit)` है। मॉडुलन सूचकांक तथा निचली पार्श्व बैण्ड आवृत्ति के मान होंगे-
View Solutionदो रेडियोधर्मी नाभिकों A तथा B की अर्द्धआयु क्रमश: 10 मिनट तथा 20 मिनट है। यदि एक नमूने में आरम्भ में दोनों नाभिकों की संख्या बराबर है, तो 60 मिनट पश्चात् A तथा B क्षयित नाभिकों की संख्या का अनुपात होगा-
View Solutionएक पिण्ड के पृथ्वी तथा एक-दूसरे ग्रह की सतह पर भारों का अनुपात 9:4 है। दूसरे ग्रह का द्रव्यमान, पृथ्वी के द्रव्यमान का `1/9` है। यदि पृथ्वी की त्रिज्या R है, तो ग्रह की त्रिज्या क्या होगी? (माना कि दोनों ग्रहों का द्रव्यमान घनत्व समान है)
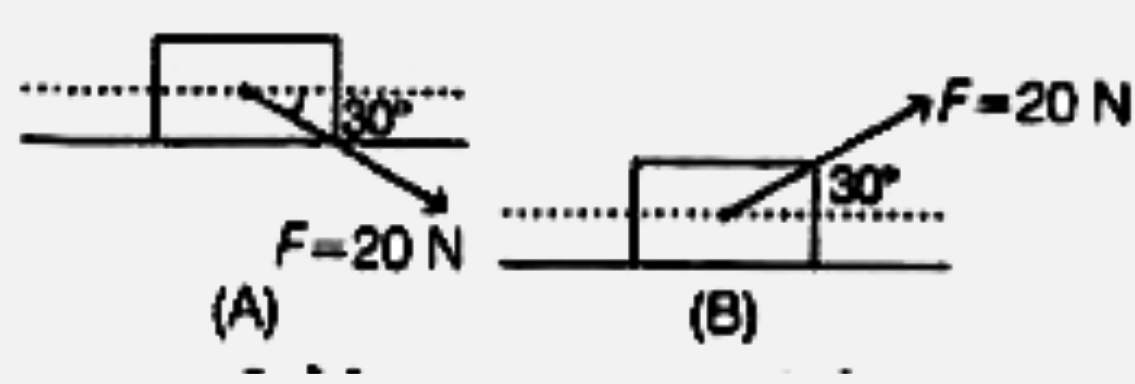
View Solution5 किग्रा के एक गुटके को क्षैतिज से 30° कोण पर बल F = 20 न्यूटन से चित्रानुसार (i) दशा (A) में धकेलते हैं तथा (ii) दशा (B) खींचते हैं। गुटके तथा समतल के बीच घर्षण गणांक `mu = 0.2` है। इन दो दशाओं (A) तथा (B) में गुटके के त्वरणों के अन्तर का मान होगा `(g = 10 "मी//से^(2))`
View Solutionएक कानों इन्जन की क्षमता `1/6` है। जब ऊष्मा कुण्ड (sink) का तापमान 62°C कम किया जाता है, तो क्षमता दोगुनी हो जाती है। ऊष्मा स्रोत तथा कुण्ड के तापमान क्रमशः होंगे-
View Solutionदो ध्वनि स्रोत `S_(1)` तथा `S_(2)` एक ही आवृत्ति 660 Hz की ध्वनि उत्पन्न करते हैं। एक श्रोता `S_(1)` से `S_(2)` की तरफ स्थिर गति `mu` मी/से से जाते हुए प्रति सेकण्ड 10 विस्पन्द सुनता है। यदि ध्वनि की गति 330 मी/से है, तो u का मान होगा-
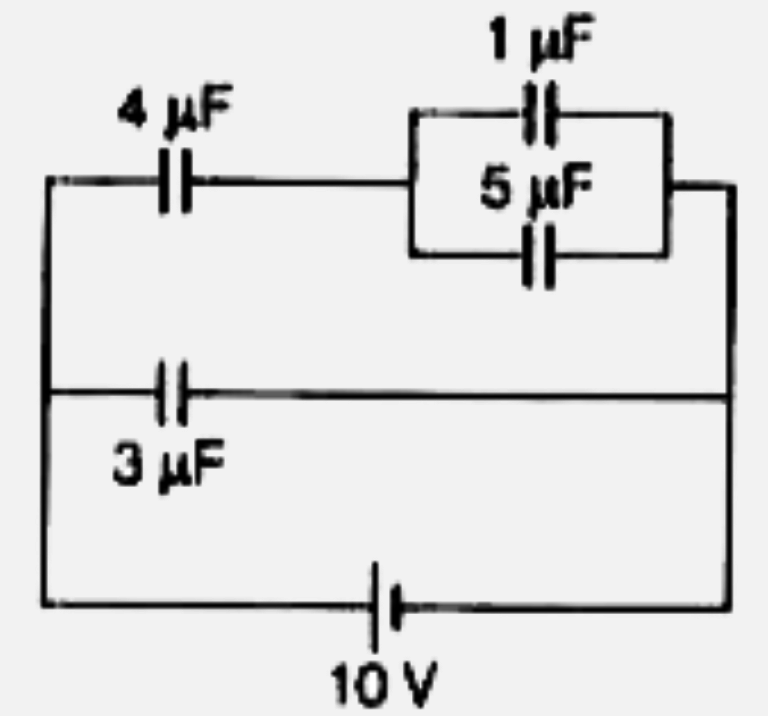
View Solutionदिए गए परिपथ 1 uF में 4gF धारिता 4uF के संधारित्र पर 5uF आवेश का मान होगा-
View Solutionप्रतिरोध G के एक चल कुण्डली धारामापी में धारा `I_(g)` पर पूर्ण विक्षेप पाया जाता है। इस धारामापी को परास 0 से `I_(0) ( I_(0) gt I_(g))` धारा के अमीटर में एक शण्ट प्रतिरोध R लगाकर परिवर्तित कर सकते हैं। इसी धारामापी को परास 0 से `V(V=GI_(0))` के वोल्टमीटर में एक श्रेणी प्रतिरोध Ry लगाकर परिवर्तित कर सकते हैं। तब-
View Solutionएक छोटे स्पीकर से 2 वाट शक्ति की ध्वनि निकलती है। इस स्पीकर से कितनी दूरी पर ध्वनि तीव्रता 120 dB होगी? [दिया है, ध्वनि की निर्देश (reference) तीव्रता `=10^(-12) W//m^(2)`)
View Solutionएक हाइड्रोजन परमाणु में इलेक्ट्रॉन दूसरी उत्तेजित कक्षा में घूम रहा है (इस कक्षा की त्रिज्या 4.65 Å है)। इस इलेक्ट्रॉन की दे-ब्रॉग्ली तरंगदैर्ध्य होगी|
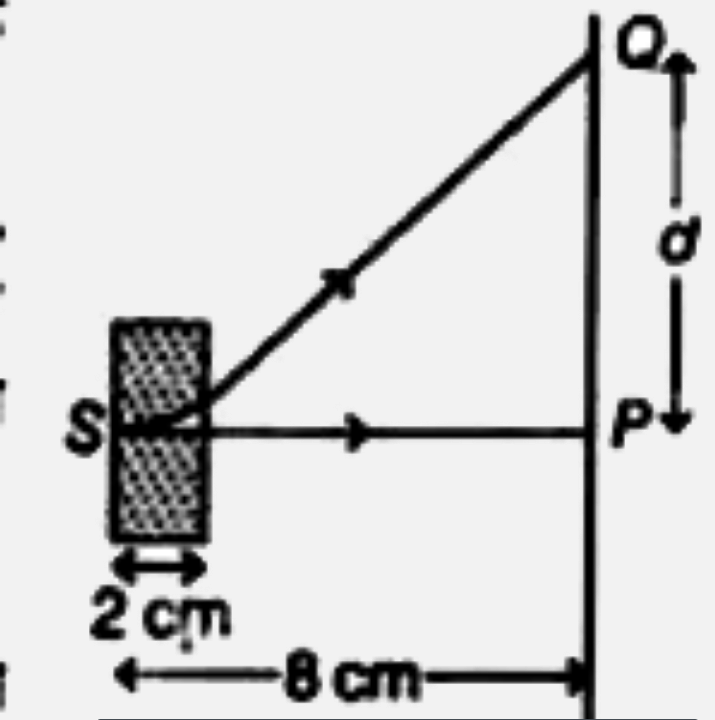
View Solution100 ev ऊर्जा का एक इलेक्ट्रॉन जो X-अक्ष के अनुदिश गतिमान है, `B=1.5 xx 10^(-3)` टेस्ल, T) `hat k` के चुम्बकीय क्षेत्र - में बिन्दु पर प्रवेश करता है (चित्र देखिए)। चुम्बकीय क्षेत्र -8 cm x=0 से x = 2 सेमी तक विस्तृत है। बिन्दु S से 8 सेमी दूरी पर स्थित पर्दे पर इलेक्ट्रॉन का संसूचन बिन्दु पर होता है। बिन्दु P तथा Q के बीच की दूरीd (पर्दे पर) का मान होगा (इलेक्ट्रॉन का आवेश = `1.6 xx 10^(-19)` कूलॉम, इलेक्ट्रॉन का द्रव्यमान = `9.1 xx 10^(-31)` किग्रा)
View Solution50 ग्राम, 100 ग्राम तथा 150 ग्राम के तीन कणों को चित्रानुसार 1 मीटर भुजा वाले एक समबाहु त्रिभुज के कोनों पर रखा है। इस निकाय के द्रव्यमान केन्द्र (x तथा y) के निर्देशांक होंगे-
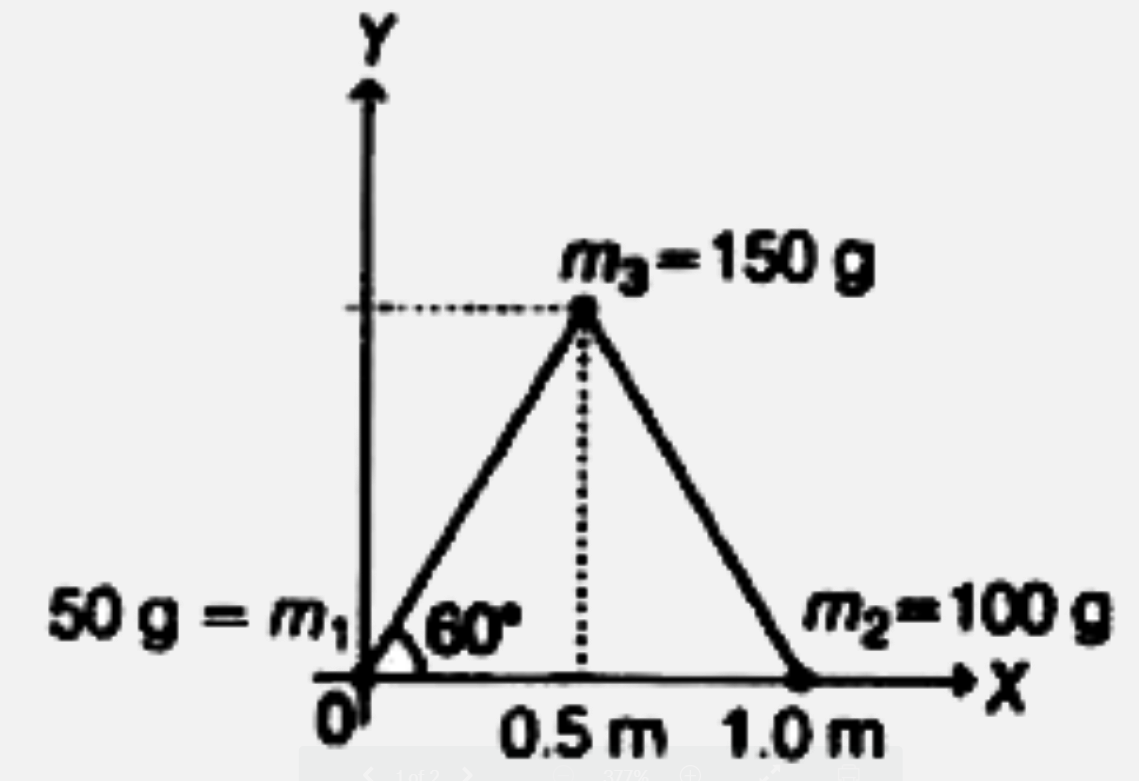
View Solutionमुक्त अवस्था में v = 23.9 GHz की एक समतल विद्युत चुम्बकीय तरंग धनात्मक 2-अक्ष की दिशा में संचरण कर रही है। इसमें विद्युत क्षेत्र का अधिकतम मान 90 V/m है। निम्न में से कौन-सा विकल्प इस तरंग के चुम्बकीय क्षेत्र के लिए स्वीकार्य है?
View Solution5 ऐम्पियर धारा के एक सीधे तार के 6 सेमी लम्बे खण्ड AB के कारण (चित्रानुसार) बिन्दु P पर चुम्बकीय क्षेत्र ज्ञात कीजिए।
`mu_(0) = 4pi xx 10^(-7) NA^(-2)`
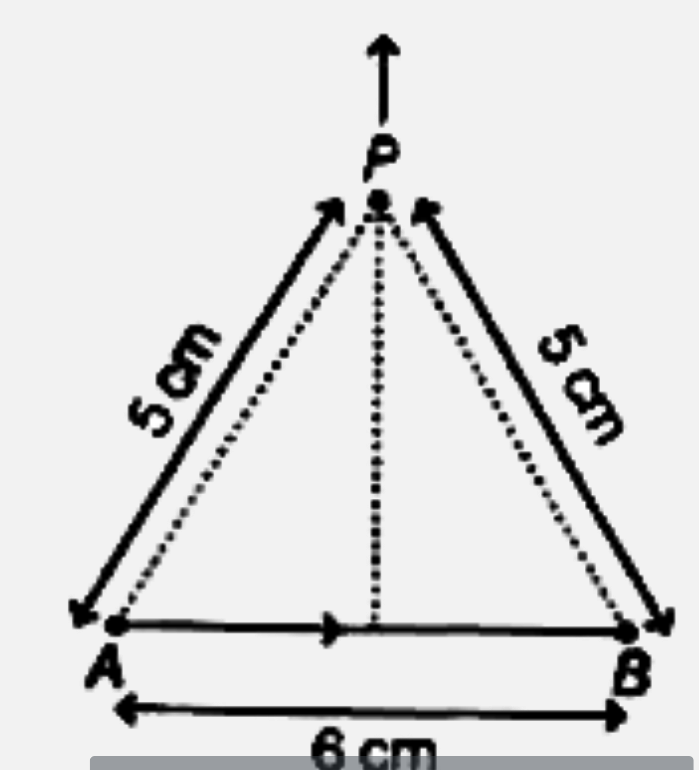
View Solution`2pi r` लम्बाई के एक घर्षणरहित तार को वृत्त बनाकर ऊर्ध्वाधर समतल में रखा है। एक मणिका (bead) इस तार पर फिसलती है। वृत्त को एक ऊर्ध्वाधर अक्ष AB के परितः चित्रानुसार कोणीय वेग `omega` से घुमाया जाता है, तो वृत्त के सापेक्ष मणिका चित्रानुसार बिन्दु P पर स्थिर पाई जाती है। `omega^(2)` का मान
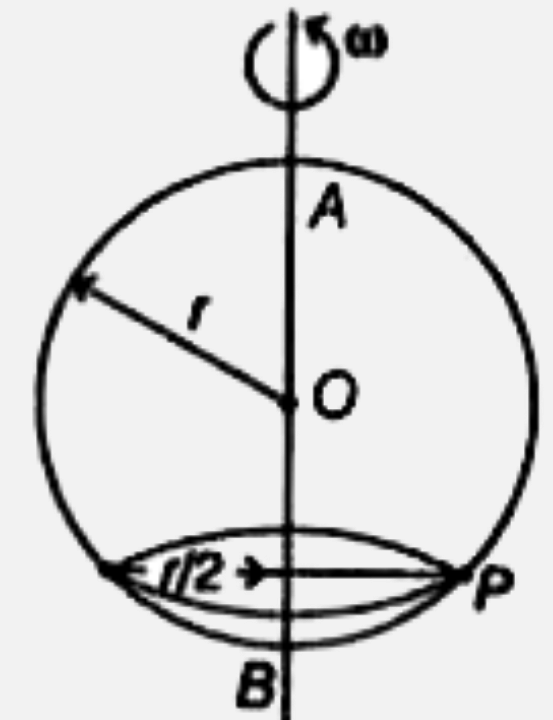
View Solutionतीन ध्रुवकों `P_(1), P_(2)` तथा `P_(3)` को इस तरह रखते हैं कि `P_(3)` की पास-अक्ष से की पास-अक्ष से क्रॉसित है। `P_(1)` की पास-अक्ष `P_(3)` की पास-अक्ष से 60° कोण पर है। जब एक `I_(0)` तीव्रता का अध्रुवित प्रकाश किरण पुँज पर आपतित होता है, तो इस तीन ध्रुवकों के समायोजन से `P_(1)` तीव्रता का प्रकाश किरण पुँज निर्गत होता है। अनुपात `I_(0)/I` का निकटतम मान होगा |
View Solution
APRIL ATTEMPT (10 APRIL, SHIFT-II) questions and complete solutions for chapter JEE MAIN 2019 (APRIL & JANUARY ATTEMPT) of ARIHANT PHYSICS (HINDI) of Class 12
All Exercises from ARIHANT HINDI Class 12 PHYSICS JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)
- APRIL ATTEMPT (10 APRIL, SHIFT-I)
- APRIL ATTEMPT (10 APRIL, SHIFT-II)
- APRIL ATTEMPT (9 APRIL, SHIFT-I)
- APRIL ATTEMPT (9 APRIL, SHIFT-II)
- APRIL ATTEMPT 8 APRIL, SHIFT-I
- APRIL ATTEMPT 8 APRIL, SHIFT-II
- JANUARY ATTEMPT (10 JAN, SHIFT -I)
- JANUARY ATTEMPT (10 JAN, SHIFT -II)
- JANUARY ATTEMPT (11 JAN, SHIFT -I)
- JANUARY ATTEMPT (11 JAN, SHIFT -II)
- JANUARY ATTEMPT (12 JAN, SHIFT -I)
- JANUARY ATTEMPT (12 JAN, SHIFT -II)
- JANUARY ATTEMPT (9 JAN, SHIFT -I)
- JANUARY ATTEMPT (9 JAN, SHIFT -II)