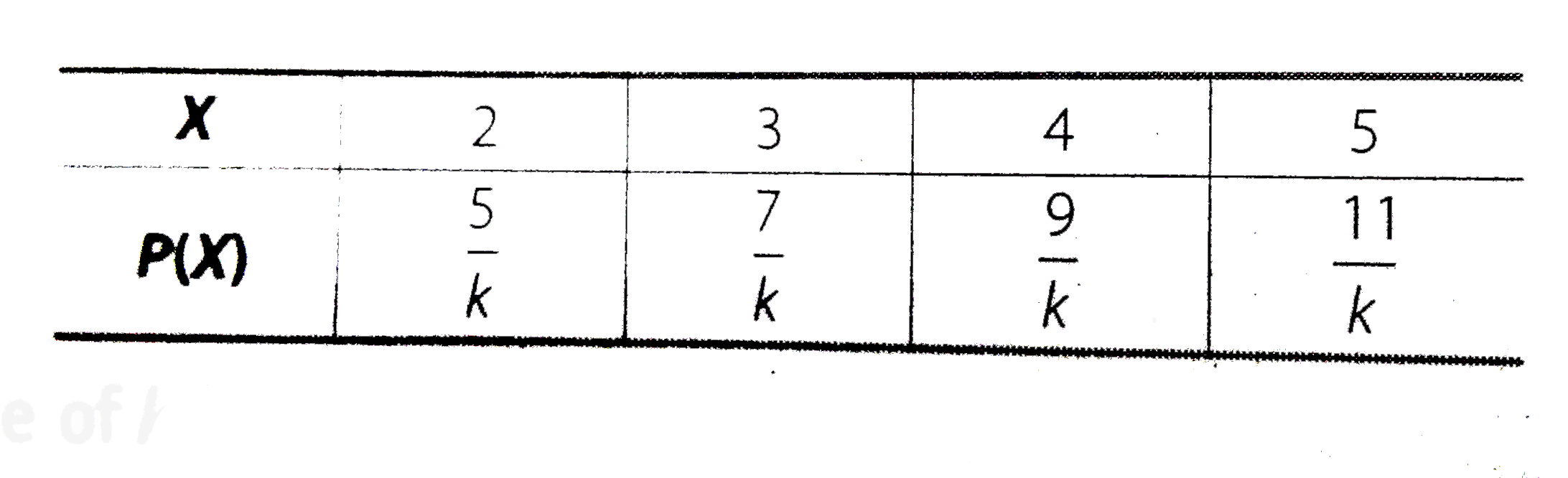Two probability distributionof the discrete random variable X and Y are given below.

Prove that E(Y2)=2E(X).
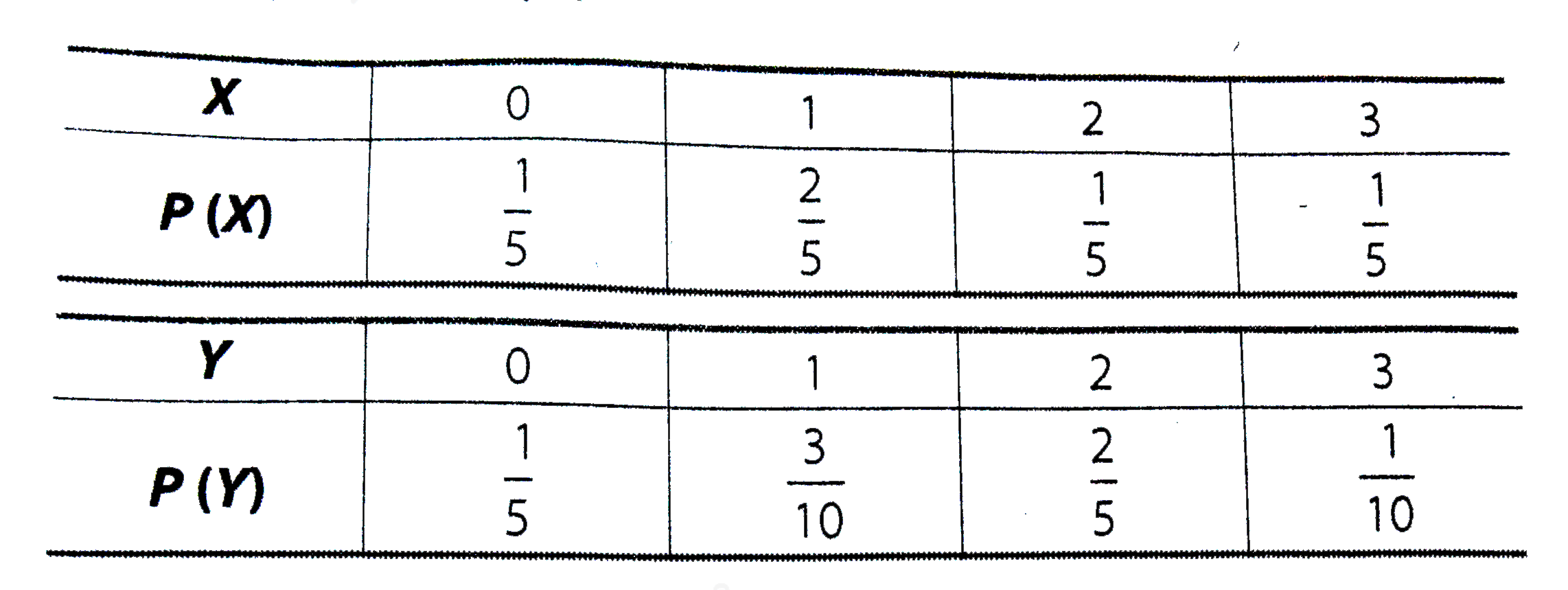
Since, we have to prove that, E(Y2)=2E(X) ltbr gtE(X)=ΣXP(X)
=0⋅15+1⋅25+3⋅15=75
⇒2E(X)=145
E(Y2)=ΣY2P(Y)
=0⋅15+1⋅310+4⋅25+9⋅110
=310+85+910=2810=145
⇒E(Y2)=145
From Eqs. (i) and (ii),
E(Y2)=2E(X) Hence proved.
Topper's Solved these Questions
- PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:PROBABILITYExercise:Long Answer Type Questions
Explore 15 Videos
- PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:PROBABILITYExercise:Objective Type Questions
Explore 38 Videos
- MATRICESBook:NCERT EXEMPLAR ENGLISHChapter:MATRICESExercise:Solved example
Explore 101 Videos
- RELATIONS AND FUNCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Fillers
Explore 15 Videos
Similar Questions
Knowledge Check
The probability distribution of the discrete random variable X is shown in the table below. What is the expected value of X?
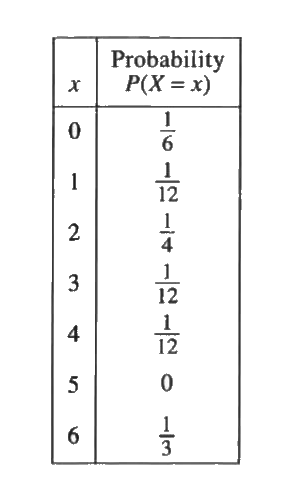 A16B13C1D316
A16B13C1D316
The probability distribution of a discrate random variable X is given below :
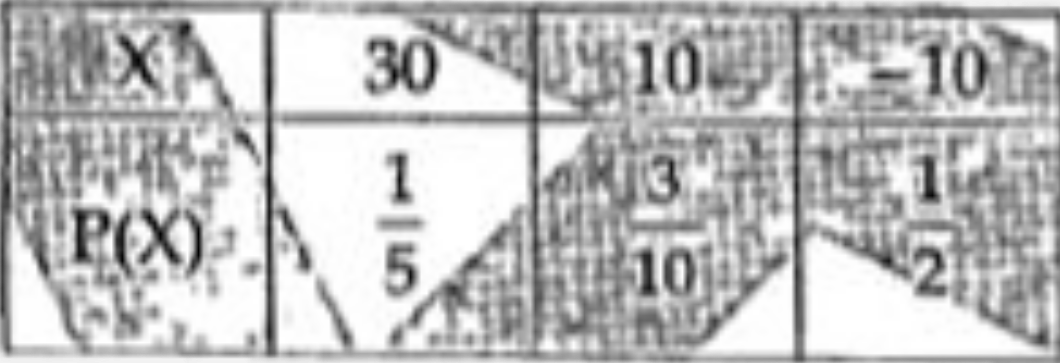
Then E(X) is equal to
View SolutionThe probability distribution of a random variable X is given below.

Find k, mean and variance of X
View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is
View SolutionConsider the probability distribution of a random variable X.

V(X2)
View SolutionThe probability distribution of a discrete random variable x is given as under
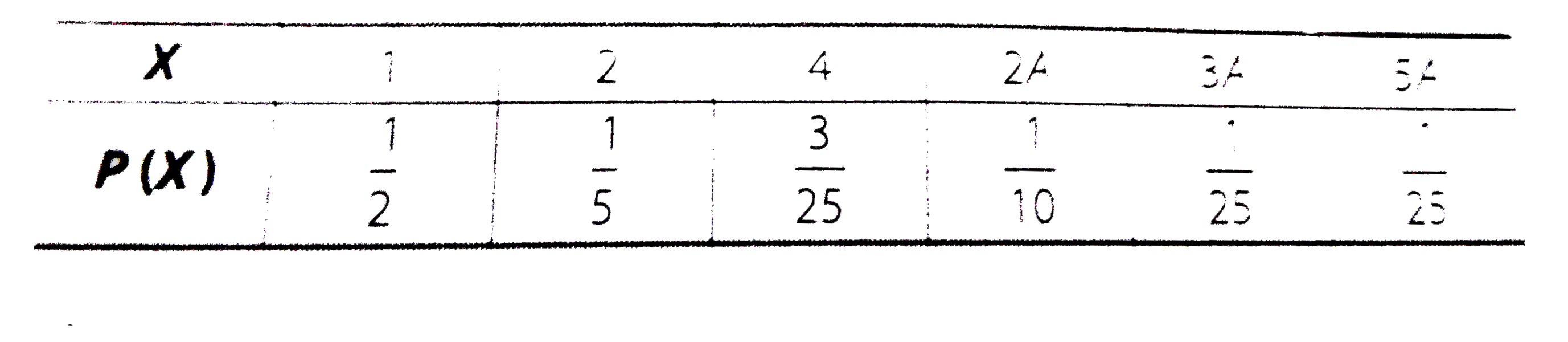
Calculate
(i) the value of A, if E(X)=2.94.
(ii) variance of X.
View SolutionThe probability of a random variable X is given below

Determine P(X≤2) and P(X>2)
View SolutionThe probability of a random variable X is given below
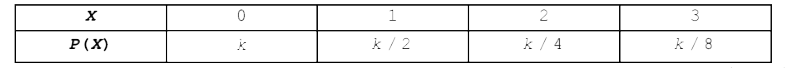
Find P(X≤2)+P(X>2)
View Solution