The probability distribution of a random variable x is given as under
P(X=x)=⎧⎪⎨⎪⎩kx2x=1,2,32kxx=4,5,60,otherwise
where, k is a constant. Calculate
(i) E(X) (ii) E(3X2) (iii) P(X≥4)
To solve the problem step by step, we will follow the instructions given in the video transcript and calculate each part accordingly.
Given Probability Distribution:
The probability distribution of a random variable X is defined as:
- P(X=x)=kx2 for x=1,2,3
- P(X=x)=2kx for x=4,5,6
- P(X=x)=0 otherwise
Step 1: Find the value of k
To find k, we need to ensure that the total probability sums to 1:
∑P(X=x)=1
Calculating each probability:
- For x=1:P(X=1)=k(12)=k
- For x=2:P(X=2)=k(22)=4k
- For x=3:P(X=3)=k(32)=9k
- For x=4:P(X=4)=2k(4)=8k
- For x=5:P(X=5)=2k(5)=10k
- For x=6:P(X=6)=2k(6)=12k
Now summing these probabilities:
k+4k+9k+8k+10k+12k=44k
Setting the sum equal to 1:
44k=1⟹k=144
Step 2: Calculate E(X)
The expected value E(X) is calculated using the formula:
E(X)=∑x⋅P(X=x)
Calculating E(X):
E(X)=1⋅k+2⋅4k+3⋅9k+4⋅8k+5⋅10k+6⋅12k
Substituting k=144:
E(X)=1⋅144+2⋅4⋅144+3⋅9⋅144+4⋅8⋅144+5⋅10⋅144+6⋅12⋅144
Calculating each term:
=144+844+2744+3244+5044+7244
Summing these:
=1+8+27+32+50+7244=19044=9522
Step 3: Calculate E(3X2)
To find E(3X2):
E(3X2)=3⋅E(X2)
Calculating E(X2):
E(X2)=∑x2⋅P(X=x)
Calculating E(X2):
E(X2)=12⋅k+22⋅4k+32⋅9k+42⋅8k+52⋅10k+62⋅12k
Substituting k=144:
E(X2)=1⋅144+4⋅4⋅144+9⋅9⋅144+16⋅8⋅144+25⋅10⋅144+36⋅12⋅144
Calculating each term:
=144+1644+8144+12844+25044+43244
Summing these:
=1+16+81+128+250+43244=90844=22711
Now, calculating E(3X2):
E(3X2)=3⋅22711=68111
Step 4: Calculate P(X≥4)
To find P(X≥4):
P(X≥4)=P(X=4)+P(X=5)+P(X=6)
Calculating each probability:
P(X=4)=8k,P(X=5)=10k,P(X=6)=12k
Substituting k=144:
P(X=4)=8⋅144=844,P(X=5)=10⋅144=1044,P(X=6)=12⋅144=1244
Summing these:
P(X≥4)=8+10+1244=3044=1522
Final Answers:
(i) E(X)=9522
(ii) E(3X2)=68111
(iii) P(X≥4)=1522
The probability distribution of a random variable X is defined as:
- P(X=x)=kx2 for x=1,2,3
- P(X=x)=2kx for x=4,5,6
- P(X=x)=0 otherwise
- For x=1:P(X=1)=k(12)=k
- For x=2:P(X=2)=k(22)=4k
- For x=3:P(X=3)=k(32)=9k
- For x=4:P(X=4)=2k(4)=8k
- For x=5:P(X=5)=2k(5)=10k
- For x=6:P(X=6)=2k(6)=12k
(i) E(X)=9522
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Objective Type Questions38videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - True/False9videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - True/False9videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example101videos
MATRICES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Fillers15videos
RELATIONS AND FUNCTIONS
Similar Questions
The probability distribution of a random variable X is given as under:

Find k , and P (X<6) .View SolutionThe probability distribution of a random variable X is given as under: P(X=x)={kx2forx=1,2,32kxforx=4,5,60otherwise , where k is a constant. Find (i) P(X≥4 ) (ii) E(X) (iii) E(3X2)
View SolutionThe probability of a random variable X is given below
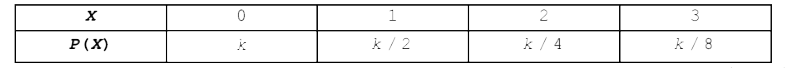
Find P(X≤2)+P(X>2)View SolutionThe probability distribution of a random variable (X) is P(X)={x12:X=1, 2, 3, 4, 5, 60:otherwise
Then, the conditional probability
P⎛⎝32<X<72X>2⎞⎠ isView SolutionThe probability distribution for a random variable X is as follows:
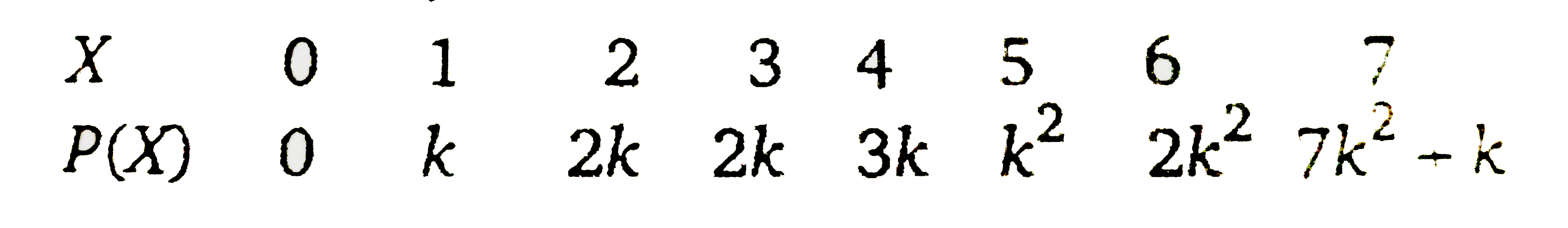
Find:
(i) k (ii) P(X<3) (iii) P(X>6)(iv)P(0X<3)View SolutionThe probability of a random variable X is given below

Determine P(X≤2) and P(X>2)View SolutionThe probability distribution of a random variable X is given by.
X=x:01234P(X=x):0.40.30.10.10.1
The variance of X, isView SolutionThe probability distribution of a random variable is given below:
X=x01234567P(X=x)0k2k2k3kk22k27k2+k
Then P(0<X<5)=View SolutionThe probability distribution of a discrete random variable x is given as under
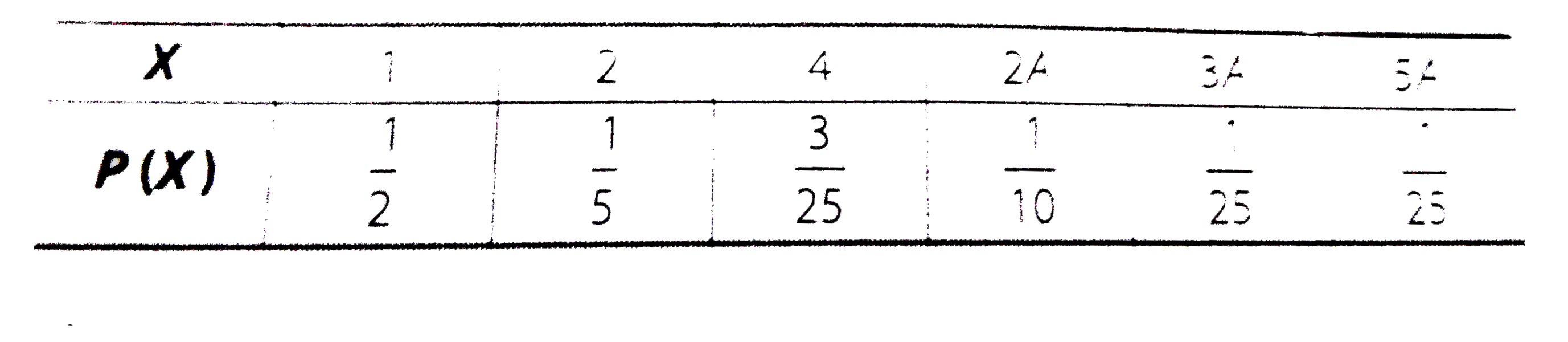
Calculate
(i) the value of A, if E(X)=2.94.
(ii) variance of X.View SolutionConsider the probability distribution of a random variable X

Calculate
(i) V(X2) (ii) Variance of X.View Solution

