Suppose the amount of milk sold daily at a milk booth is distributed with a minimum of 200 litres and a maximum of 600 litres with probability density function
f(x)={k200≤x≤6000otherwise
Find
the distribution functionSolution in Tamil
Step by step video & image solution for Suppose the amount of milk sold daily at a milk booth is distributed with a minimum of 200 litres and a maximum of 600 litres with probability density function f(x)={{:(k, 200 le x le 600), (0, "otherwise"):} Find the distribution function by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE 11.411videos
PROBABILITY DISTRIBUTIONS
- BOOK - PREMIERS PUBLISHERSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE 11.518videos
PROBABILITY DISTRIBUTIONS
- BOOK - PREMIERS PUBLISHERSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE 11.218videos
PROBABILITY DISTRIBUTIONS
- BOOK - PREMIERS PUBLISHERSCHAPTER - ORDINARY DIFFERENTIAL EQUATIONS EXERCISE - PROBLEMS FOR PRACTICE (ANSWER THE FOLLOWING QUESTIONS )22videos
ORDINARY DIFFERENTIAL EQUATIONS
- BOOK - PREMIERS PUBLISHERSCHAPTER - THEORY OF EQUATIONSEXERCISE - Problems for practice (Answer the following)21videos
THEORY OF EQUATIONS
Similar Questions
For the random variable X with the given probability mass function as below, find the mean and variance.
f(x)=⎧⎨⎩110x=2,515x=0,1,3,406:02View SolutionCompute P(X=K) for the binomial distribution B(n,p) where
n=6,p=13,k=302:36View SolutionThree fair coins are tossed simultaneously. Find the probability mass function for number of heads occurred.
02:52View SolutionFind the order and degree of the following differential equation
y''=(2+y')3404:39View SolutionIf α and β are the roots of 2x2−5x+3=0 form the equation whose roots are α2 and β2
02:09View SolutionFollowing is the distribution function F(x) of a X.

Find P(X≤3),P(2≤X≤5)01:54View SolutionShow that the function f(x) defined by .f(x)=17, for 1≤x≤8 =0, otherwise, is a probability density function for a random variable. Hence find P(3<X<10)
04:09View SolutionProbability distribution of X is given by
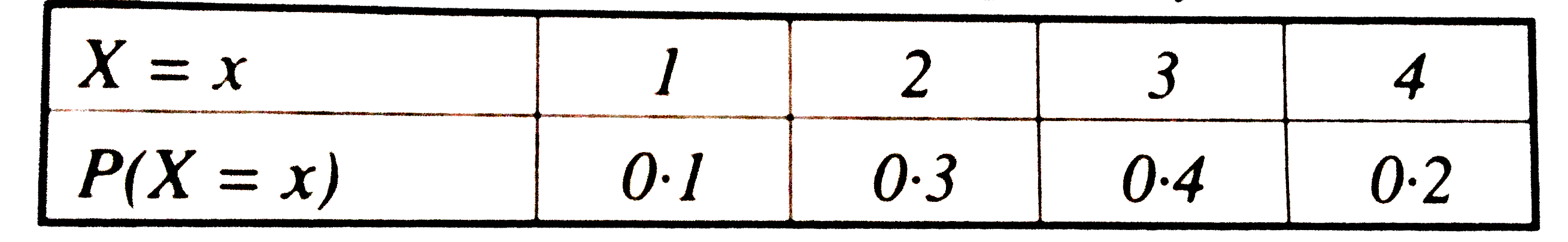
Find P(X≤2) and obtain cumulative distribution function of X.02:55View SolutionThe probability density function of X is given by f(x)={kxe−2xfor x>00for x≤0 Find the value of k.
03:51View SolutionThe probability density function of X is
f(x)=⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find
P(0.2≤X<0.6)03:08View SolutionThe probability density function of X is
f(x)=⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find
P(1.2≤X<1.8)01:57View SolutionThe probability density function of X is
f(x)=⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find
P(0.5≤X<1.5)02:52View SolutionSuppose the amount of milk sold daily at a milk booth is distributed with a minimum of 200 litres and a maximum of 600 litres with probability density function
f(x)={k200≤x≤6000otherwise
Find
the value of k10:47View SolutionSuppose the amount of milk sold daily at a milk booth is distributed with a minimum of 200 litres and a maximum of 600 litres with probability density function
f(x)={k200≤x≤6000otherwise
Find
the distribution function01:38View SolutionSuppose the amount of milk sold daily at a milk booth is distributed with a minimum of 200 litres and a maximum of 600 litres with probability density function
f(x)={k200≤x≤6000otherwise
Find
the probability that daily sales will fall between 300 litres and 500 litres?05:25View SolutionThe probability density function of X is given by f(x)={ke−x3for x>00for x≤0
Find
the value of k05:14View Solution

