Suppose be three mutually exclusive events such that .
P(none of ) equals
0
1-
None of these
The correct Answer is:(b)
Step by step video & image solution for Suppose E_1, E_2 and E_3 be three mutually exclusive events such that P(E_i)=p_i" for " i=1, 2, 3. P(none of E_1, E_2, E_3) equals by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Single Integer Answer Type Questions)10videos
PROBABILITY
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Probability Exercise 5: Match Type Questions5videos
PROBABILITY
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (More Than One Correct Option Type Questions)15videos
PROBABILITY
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)28videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)51videos
PRODUCT OF VECTORS
Similar Questions
Suppose E1,E2andE3 be three mutually exclusive events such that P(Ei)=pi for i=1,2,3.
If p1,p2andp3 are the roots of 27x3−27x2+ax−1=0 the value of a isView SolutionSuppose E1,E2andE3 be three mutually exclusive events such that P(Ei)=pi for i=1,2,3.
P(E1∩¯¯¯¯E2)+P(E2∩¯¯¯¯E3)+P(E3∩¯¯¯¯E1) equalsView Solution
Knowledge Check
- Question 1 - Select One
Let E1andE2 are two mutually exclusive and exhaustive events. If odds are 2:3 against E1 then odds in favour of E2 are
A3:2B1:3C3:1D2:3 - Question 2 - Select One
If A,B,C are three mutually exclusive and exhaustive events of an experiment such 3P(A) = 2I = P(C ) , the P(A) is equal to .
A111B211C511D611
Statement -1 : Let E1,E2,E3 be three events such that P(E1)+P(E2)+P(E3)=1, then E1,E2,E3 are exhaustive events.
Statement-2 if the events E1,E2 and E3 be exhaustive events, then P(E1∪E2∪E3)=1View SolutionLet H1,H2,...,Hn be mutually exclusive events with P(Hi)>0,i=1,2,..........n. Let E be any other event with 0<P(E) Statement I P(Hi∣E)>P(E∣Hi.P(Hi) for i=1,2,.......,n statement II n∑i=1P(Hi)=1
View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E1)=12andP(E1∣E2)=14. Observe the lists given below :
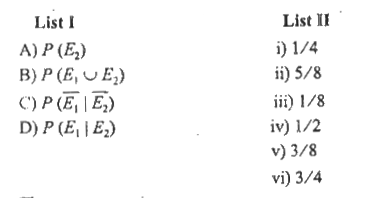
The correct matching of the list I from the list II is :View SolutionLet p (x) be a polynomial with real coefficient and p(x)=x2+2x+1. Find P (1).
View SolutionIf EandF are two events such that P(E∪F)=0.6,P(E∩F)=0.3,P(F)=0.2. Find P(notE) .
View SolutionIf E1 and E2 are two events such that P(E1)=1/4, P(E2/E1)=1/2 and P(E1/E2)=1/4, then
View Solution

