Let A and B be two events such that P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where¯¯¯A stands for the complement of the event A. Then the events A and B are
mutually exclusive and independent
equally likely but not independent
Independent but not equally likely
independent and equally likely
The correct Answer is:C
P(¯¯¯¯¯¯¯¯¯¯A∪B)=16
P(A∪B)=56,P(A)=34
P(A∪B)−P(A)+P(B)−P(A∩B)=56
⇒P(B)=56−34+14=13
⇒P(A∩B)=P(A).P(B)=14
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - JEE Advanced Previous Year25videos
PROBABILITY II
- BOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - LINKED COMPREHENSION TYPE11videos
PROBABILITY II
- BOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - Exercise (Numerical)20videos
PROBABILITY II
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - JEE Advanced Previous Year7videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
Similar Questions
Let A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14 where ¯¯¯A stands for complement of event A. Then, events A and B are
View SolutionLet A and B be two events such that
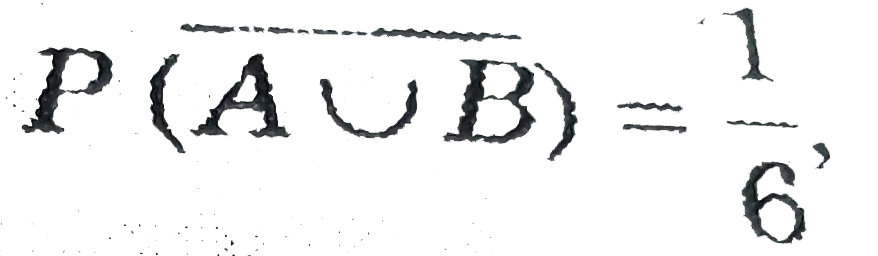,P(A cap B)=(1)/(4)andPoverset(-)(A)=(1)/(4),whereoverset(-)A stands for the complement of the event A. Then, the events A and B are View Solution
Knowledge Check
- Question 1 - Select One
Let A and B be two events such that P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where¯¯¯A stands for the complement of the event A. Then the events A and B are
Amutually exclusive and independentBequally likely but not independentCindependent but not equally likelyDindependent and equally likely - Question 2 - Select One
Let A and B be two events such that p(¯¯¯A∪B)=16,p(A∩B)=14 and p(¯¯¯A)=14 , where ¯¯¯A stands for the complement of the event A. Then the events A and B are (1) mutually exclusive and independent (2) equally likely but not independent (3) independent but not equally likely (4) independent and equally likely
Amutually exclusive and independentBequally likely but not independentCIndependent but not equally likelyDindependent and equally likely - Question 3 - Select One or More
If A and B are two events such that P(A∪B)=34, P(A∩B)=14,P(¯¯¯A)=23, then
AP(¯¯¯A∩B)=512BP(B)=23CP(¯¯¯A∪¯¯¯B)=14DP(¯¯¯A∪¯¯¯B)=34
If A and B are two events such that P((A ∪ B)')=16,P(A∩B)=14 and P(A')=14, then P(A) and P(B) are
View SolutionLet A and B be the two events such that P(A)=12,P(B)=13andP(A∩B)=14 , find
P(AB)View SolutionIf A and B are two events such that P[(A∪B)']=16,P(A∩B)=14 and P(A')=14 , then events A and B are
View SolutionLet A and B be two events such that
P(A∩B)=16,P(A∪B)=3145 and P(¯¯¯B)=710, thenView SolutionIf A and B are any two events such that P(A∪B)=34,
P(A∩B)=14andP(¯¯¯A)=23, where ¯¯¯A stands for the complementary event of A, then what is P(B) ?View Solution