In a ΔPQR, N is a point on PR, such that QN⊥PR. If PN⋅NR=QN2, then prove that ∠PQR=90∘.
Video Solution
Text Solution
Given ΔPQR, N is a point on PR, such that QN⊥PR
and PN⋅NR=QN2
To Prove ∠PQR=90∘
Proof We have , PN⋅NR=QN2
⇒PN⋅NR=QN⋅QN
⇒PNQN=QNNR
and ∠PNQ=∠RNQ
∴ΔQNP~ΔRNQ
then, ΔQNPandΔRNQ are equiangualrs.
i.e, ∠PQN=∠QRN
∠RQN=∠QPN
On adding both sides, we get
∠PQN+∠RQN=∠QRN+∠QPN
⇒∠PQR=∠QRN+∠QPN ....(ii)
We know that, sum of angles of a triangle=180∘
In ΔPQR,∠PQR+∠QPR+∠QRP=180∘
⇒∠PQR+∠QPN+∠QRN=180∘ [∵∠QPR=∠QPNand∠QRP=∠QRN]
⇒∠PQR+∠PQR=180∘ [using Eq. (ii)]
⇒2∠PQR=180∘
⇒∠PQR=180∘2=90∘
∴∠PQR=90∘ Hence proved

|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
ΔPQR is isosceles triangle with PQ = PR. If <Q=70∘, then the other angles of the triangle.
A30∘,70∘B40∘,70∘C70∘,80∘D50∘,40∘ - Question 2 - Select One
ΔPQR is an isosceles triangle with PQ=PR. If ∠Q=70∘, then find the other angles of the triangle.
A30∘,70∘B40∘,70∘C70∘,80∘D50∘,40∘ - Question 3 - Select One
PQR is an equilateral triangle. MN is drawn parallel to QR such that M is on PQ and N is on PR. If PN = 6 cm, then the length of MN is
A3 cmB6 cmC12 cmD4.5 cm
In a triangle PQR, X is a point on PR and Y is a point on QR such that PR = 10 cm, RX = 4 cm, YR = 2 cm, QR = 5 cm. Which one of the following is correct?
View SolutionIn ΔPQR,∠PQR=90∘,
seg QS⊥ seg PR then find x,y,z.View SolutionIn a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
View SolutionPQR is a triangle in which PR=QR. Side PR is extended to S, such that QR=RS. If ∠QPR=40∘, then what is the value (in degrees) of ∠QSR?
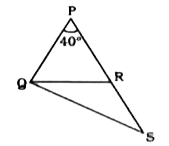 View Solution
View SolutionIn a triangle PQR, PQ=20 cm and PR =6 cm, the side QR is :
View Solution
