If the probability density function of a random variable X is f(x)=x2 in 0≤x≤2, then P(X>1.5∣X>1) is equal to
716
34
712
2164
The correct Answer is:C
To solve the problem, we need to find the conditional probability P(X>1.5|X>1) given the probability density function (PDF) f(x)=x2 for 0≤x≤2.
1. Identify the Events:
- Let A be the event X>1.5.
- Let B be the event X>1.
We need to find P(A|B), which can be calculated using the formula:
P(A|B)=P(A∩B)P(B)
2. Find P(A∩B):
- The event A∩B corresponds to X>1.5, since if X>1.5, it is also greater than 1.
- Therefore, P(A∩B)=P(X>1.5).
We calculate P(X>1.5) using the PDF:
P(X>1.5)=∫21.5f(x)dx=∫21.5x2dx
Now, we calculate the integral:
=12∫21.5xdx=12(x22)21.5
=12(222−(1.5)22)=12(42−2.252)
=12(2−1.125)=12×0.875=0.8752=716
3. Find P(B):
- Now we calculate P(B)=P(X>1):
P(X>1)=∫21f(x)dx=∫21x2dx
=12∫21xdx=12(x22)21
=12(222−122)=12(42−12)
=12(2−0.5)=12×1.5=34
4. Calculate P(A|B):
Now we can substitute the values we found into the conditional probability formula:
P(A|B)=P(A∩B)P(B)=71634=716×43=7×416×3=2848=712
Final Answer:
Thus, P(X>1.5|X>1)=712.
- Let A be the event X>1.5.
- Let B be the event X>1.
P(A|B)=P(A∩B)P(B)
- The event A∩B corresponds to X>1.5, since if X>1.5, it is also greater than 1.
- Therefore, P(A∩B)=P(X>1.5).
P(X>1.5)=∫21.5f(x)dx=∫21.5x2dx
=12∫21.5xdx=12(x22)21.5
=12(222−(1.5)22)=12(42−2.252)
=12(2−1.125)=12×0.875=0.8752=716
- Now we calculate P(B)=P(X>1):
P(X>1)=∫21f(x)dx=∫21x2dx
=12∫21xdx=12(x22)21
=12(222−122)=12(42−12)
=12(2−0.5)=12×1.5=34
Now we can substitute the values we found into the conditional probability formula:
P(A|B)=P(A∩B)P(B)=71634=716×43=7×416×3=2848=712
Thus, P(X>1.5|X>1)=712.
Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONBook:TARGET PUBLICATIONChapter:PROBABILITY DISTRIBUTIONExercise:Competitive Thinking
Explore 9 Videos
- PLANEBook:TARGET PUBLICATIONChapter:PLANEExercise:EVALUATION TEST
Explore 14 Videos
- THREE DIMENSIONAL GEOMETRY Book:TARGET PUBLICATIONChapter:THREE DIMENSIONAL GEOMETRY Exercise:Evaluation Test
Explore 9 Videos
Similar Questions
Knowledge Check
If the probability density function of a random variable X is f(x)=π2 in 0≤x≤2, then P(X>1.5X>1) is equal to
A716B34C712D2164If the p.d.f of a random variable X is
F(x)={0.5x0≤x≤20otherwise
Then the value of P(0.5≤X≤1.5) isA14B12C34D1If f(x)={|x|x≤12−xx>1, then fof (x) is equal to
Af(x)=⎧⎪⎨⎪⎩2−xx<−1|x|−1≤x≤1|2−x|x>1Bf(x)=⎧⎪⎨⎪⎩|x|x<−12−|x|−1≤x≤1|2−x|x>1Cf(x)=⎧⎪⎨⎪⎩|2−x|x<−1|x|−1≤x≤12−|x|x>1DNone of these
The probability of a random variable X is given below
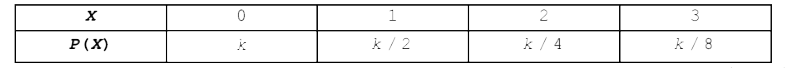
Find P(X≤2)+P(X>2)
View SolutionShow that the function f(x) defined by .f(x)=17, for 1≤x≤8 =0, otherwise, is a probability density function for a random variable. Hence find P(3<X<10)
View SolutionThe p.d.f of continuous random variable X is given by f(x)=x8,0<x<4=0 otherwise. Find (i) P(X<2)(ii)P(2<X≤3)(iii)P(X>3.)
View Solutionf(x)={3x−8ifx≤52kifx>5 at x=5
View SolutionIf f(x)=x for x≤0=0 for x>0, then f(x) at x=0 is
View Solution


