If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram, so formed will be half of the area of the given quadrilateral (figure).

Video Solution

Text Solution

Verified by Experts

Given Let ABCD is a quadrilateral and P, F, R and S are the mid-points of the sides BC, CD, AD and AB respectively and PFRS is a parallelogram.

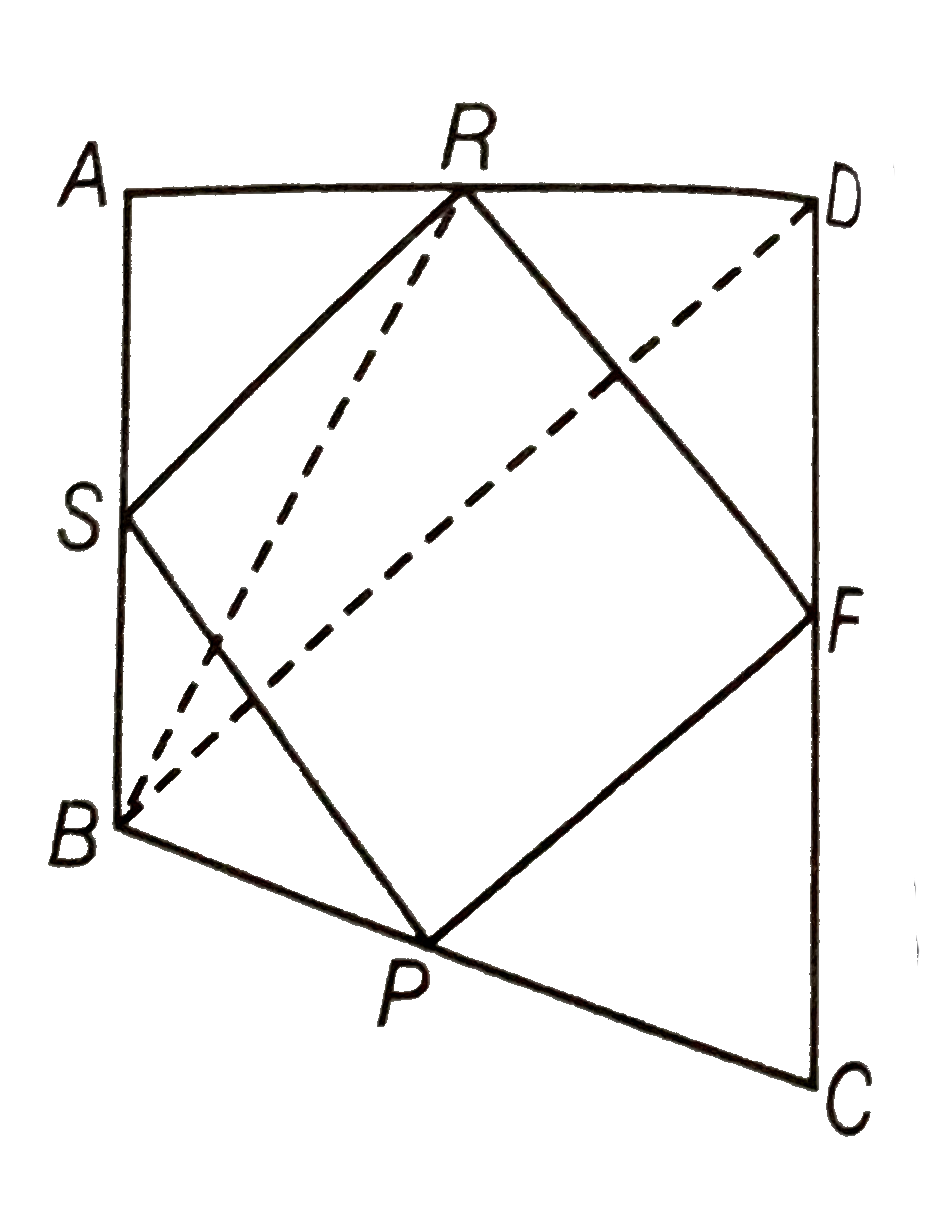
To prove ar (parallelogram PFRS) = $\frac{1}{2} a r (quadrilateral A B C D)$
Construction Join BD and BR.
Proof Median BR divides $Δ B D A$ into two triangles of equal area.
$∴$ $a r (Δ B R A) = \frac{1}{2} a r (Δ B D A)$ ...(i)
Similarly, Median RS divides $Δ B R A$ into two triangles of equal area.
$∴$ $a r (Δ A S R) = \frac{1}{2} a r (Δ B R A)$ ...(ii)
From Eqs. (i) and (ii),
$a r (Δ A S R) = \frac{1}{4} a r (Δ B D A)$ ...(iii)
Similarly, $a r (Δ C F P) = \frac{1}{4} a r (Δ B C D)$ ...(iv)
On adding Eqs. (iii) and (iv), we get
$a r (Δ A S R) + a r (Δ C F P) = \frac{1}{4} a r (Δ B D A)$ [ $a r (Δ B D A) + a r (Δ B C D)$ ]
$\Rightarrow$ $a r (Δ A S R) + a r (Δ C F P) = \frac{1}{4} a r (quadrilateral B C D A)$ ...(v)
Similarly, $a r (Δ D R F) + a r (Δ B S P) = \frac{1}{4} a r (quadrilateral B C D A)$ ...(vi)
On adding Eqs. (v) and (vi), we get
$a r (Δ A S R) + a r (Δ C F P) + a r (Δ D R F) + a r (Δ B S P)$
$= \frac{1}{2} a r (quadrilateral B C D A)$ ...(vii)
But $a r (Δ A S R) + a r (Δ C F P) + a r (Δ D R F) + a r (Δ B S P) + a r (parallelogram P F R S)$
$= a r (quadrilateral B C D A)$ ...(viii)
On subtracting Eq. (vii) from Eq. (viii), we get
$a r (parallelogram P F R S) = \frac{1}{2} a r (quadrilateral B C D A)$ Hence proved.

Updated on:21/07/2023

In the figure, the area of the quadrilateral ABCD is 75. What is the area of parallelogram EFGH?

A96
B153
C157
D171
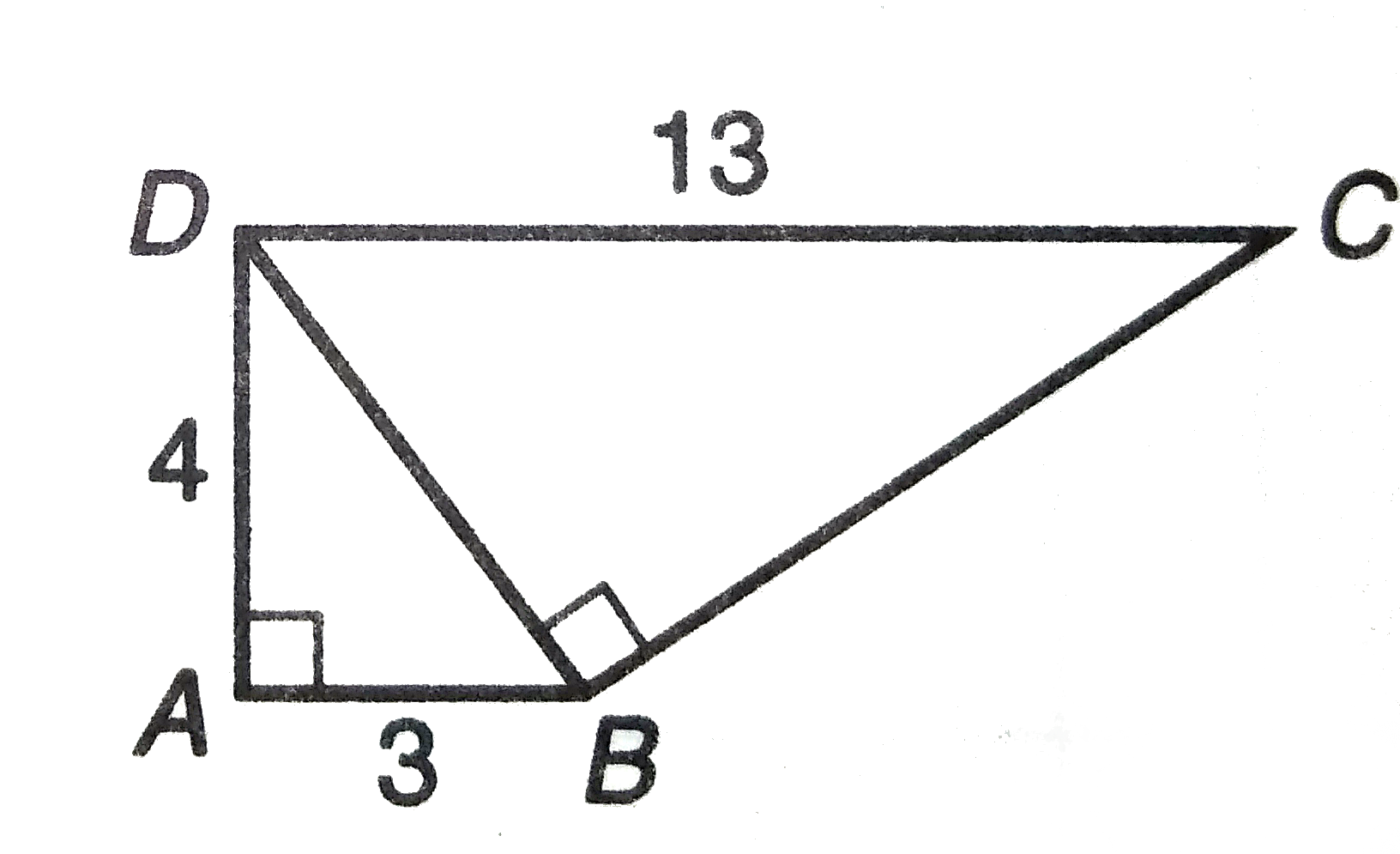
In the figure above, what is the area of quadrilateral ABCD?
A $28$
B $32$
C $36$
D $42$
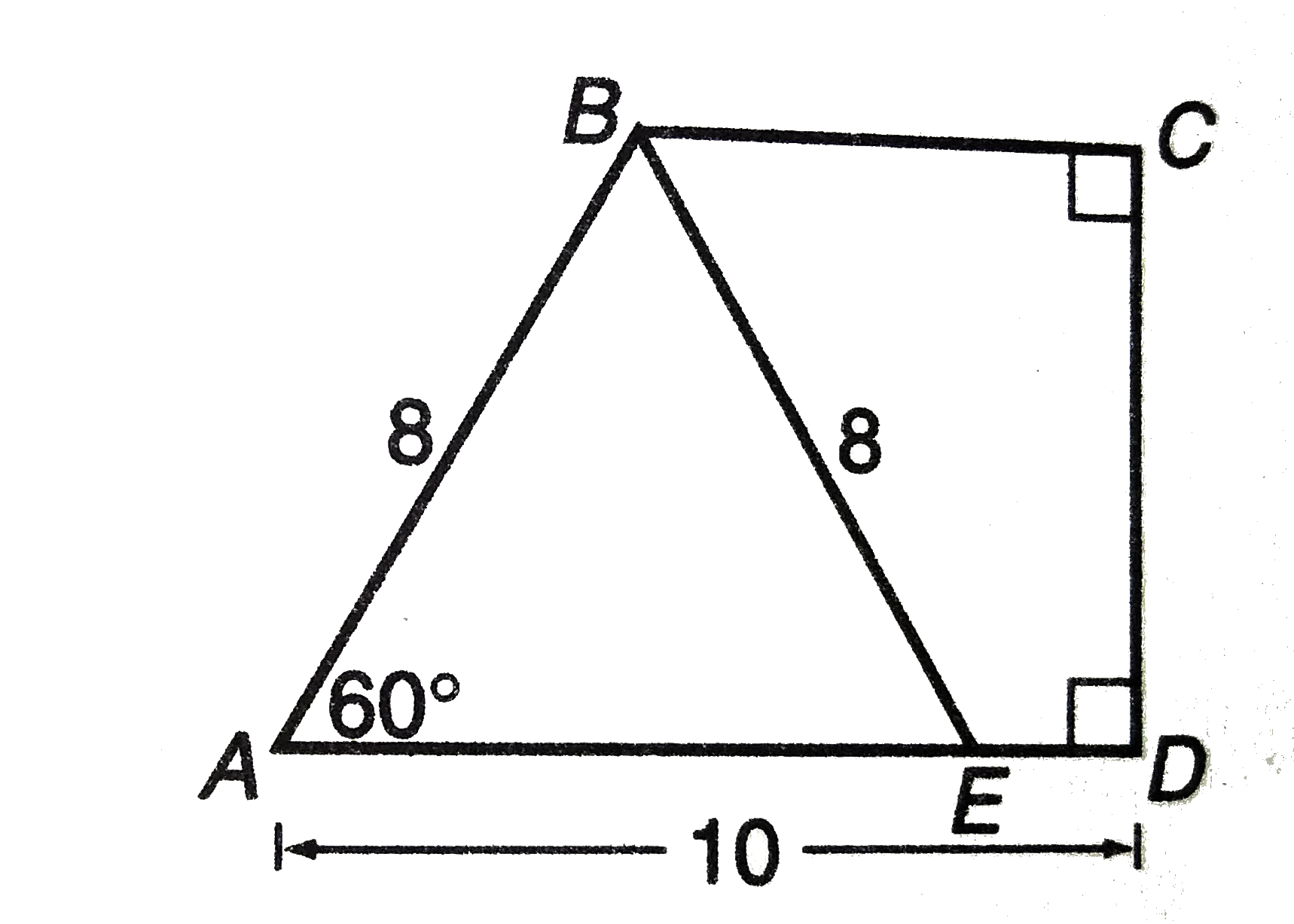
In the figure above, what is the area of quadrilateral BCDE?
A $8 \sqrt{3}$
B $16 \sqrt{3}$
C $8 + 4 \sqrt{3}$
D $4 + 12 \sqrt{3}$