If P(A)=0.8,P(B)=0.5 and P(B/A)=0.4, find
(i) P(A∩B)
(ii) P(A/B)
(iii) P(A∪B)Solution in Punjabi
Step by step video & image solution for If P(A)=0.8, P(B)=0.5 and P(B//A)=0.4, find (i) P(AnnB) (ii) P(A//B) (iii) P(AuuB) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Compute P(A∣B),if P(B)=0.5 and P(A∩B)=0.32
03:02View SolutionWrite the element a12 of the matrix A=[aij]2×2, whose elements are given by : aij=e2ixsinjx
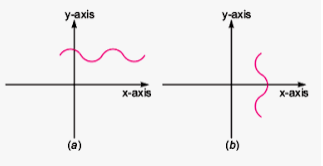
03:13View SolutionWhich one of the following graph represents the function of x? Why?
 04:01View Solution
04:01View SolutionCheck whether the following probabilities P(A) and P(B) are consistently defined
(i) P(A)=0.5,P(B)=0.7,P(A∩B)=0.6
(ii) P(A)=0.5,P(B)=0.4,P(A∪B)=0.802:50View SolutionIf A and B are two events such that P(A)=0.4,P(B)=0.8 and P(B/a)=0.6, then find:
(i) P(A∩B) (ii) P(A∪B) (iii) P(A/B)02:17View Solutionयदि P(A)=0.8,P(B)=0.5 और P(B∣A)=0.4 ज्ञात कीजिए
(i) P(A∩B) (ii) P(A∣B) (iii) P(A∪B)02:33View Solutionजांच कीजिए कि निम्न प्रायिकताएं P(A) और P(B) युक्ति संगत परिभाषित की गइ है
(i) P(A)=0.5,P(B)=0.7,P(A∩B)=0.6
(ii) P(A)=0.5,P(B)=0.4,P(A∪B)=0.802:43View SolutionCheck whether the following probabilities P(A) and P(B) the consistently defined:
(i) P(A)=0.5,P(B)=0.7,P(A∩B)=0.06
(ii) P(A)=0.5,P(B)=0.4,P(A∪B)=0.802:47View SolutionCheck whether the following probabilities P(A) and P(B) the consistently defined:
(i) P(A)=0.5,P(B)=0.7,P(A∩B)=0.06
(ii) P(A)=0.5,P(B)=0.4,P(A∪B)=0.802:18View SolutionIf P(A)=0.8,P(B)=0.5 and P(B/A)=0.4, find (i) P(A∩B) (ii) P(A/B) (iii) P(A∪B).
02:34View SolutionIf P(A) = 0.8, P(B) = 0.5 and P(B|A) = 0.4 Find i. P(A∩B) ii. P(A|B) iii. P(A∪B)
03:30View SolutionIf P(A)= 0.8, P(B) = 0.5 and P(B|A) = 0.4, find
i. P(A∩B) ii. P(A|B) iii. P(A∪B)02:13View SolutionIf P(A) = 0.8, P(B) = 0.5 and P (B|A) = 0.4, find
(i) P(A∩B) (ii) P(A|B) (iii) P(A∪B)03:21View SolutionIf P(A) = 0.8, P(B) = 0.5 and P (B|A) = 0.4, find
(i) P(A∩B) (ii) P(A|B) (iii) P(A∪B)02:29View SolutionIf P(A) = 0.8, P(B) = 0.5 and P (B|A) = 0.4, find
(i) P(A∩B) (ii) P(A|B) (iii) P(A∪B)02:44View SolutionCheck whether the following probabilities P(A) and P(B) are consistently defined
(i) P(A)=0.5,P(B)=0.7,P(A∩B)=0.6
(ii) P(A)=0.5,P(B)=0.4,P(A∪B)=0.803:00View Solution

