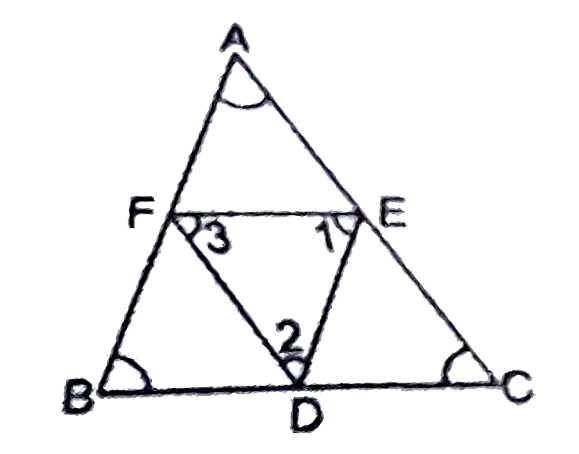
If D,E,F are the mid-points of the sides BC,CAandAB respectively of a triangle ABC, prove by vector method that AreaofDEF=14(areaofABC).
Given: △ABC in which , D E and F are mid-point if the sides, BC, CA and AB respectively.
To porve: To determine the ratio of the areas of △DEFand△ABC
proof: Since D,E,F are the mid-point
EF||BC and EF=12BC
EF=BD
Similarly, DE= BF ( DE∣∣ABand12AB)
So, EFBD is a parallelogram.
∠B=∠1
Similarly , AFDE and EFDC and parallelogram
⇒∠A=∠2and∠C=∠3
i.e.△ABCand△DEF are equiangular
⇒△DEF~△ABC
ar(△DEF)ar(△ABC)=DE2(AB2)=FB2AB2=(AB/2)2AB2=14
Hence ((ar(triangleDEF))/((ar(trangleABC))= 1/4
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar14videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a24videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions4videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
If D, E, F are the mid points of the side BC, CA and AB respectively of a triangle ABC, write the value of →AD+→BE+→CF.
View SolutionD, E, F are the mid-points of the sides BC, CA and AB respectively of a ΔABC . Determine the ratio of the areas of DEF and ABC .
View SolutionIf D,EandF are three points on the sides BC,CAandAB, respectively, of a triangle ABC show that the BDCD=CEAE=AFBF=−1
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of △ABC. Then DEF is congruent to triangle.
(a)ABC
(b) AEF
(c) BFD, CDE
(d) AFE, BFD, CDEView SolutionLet ABC be an isosceles triangle in which AB=AC. If D, E, F be the mid-points of the sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE triset (divide into three equal parts) the diagonal BD.
View SolutionIf D, E and F are the mid-points of the sides of a △ABC , the ratio of the areas of the triangles DEF and ABC is .......
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(△ADF)=ar(△DCE).
View Solution
