For the following probability distribution.
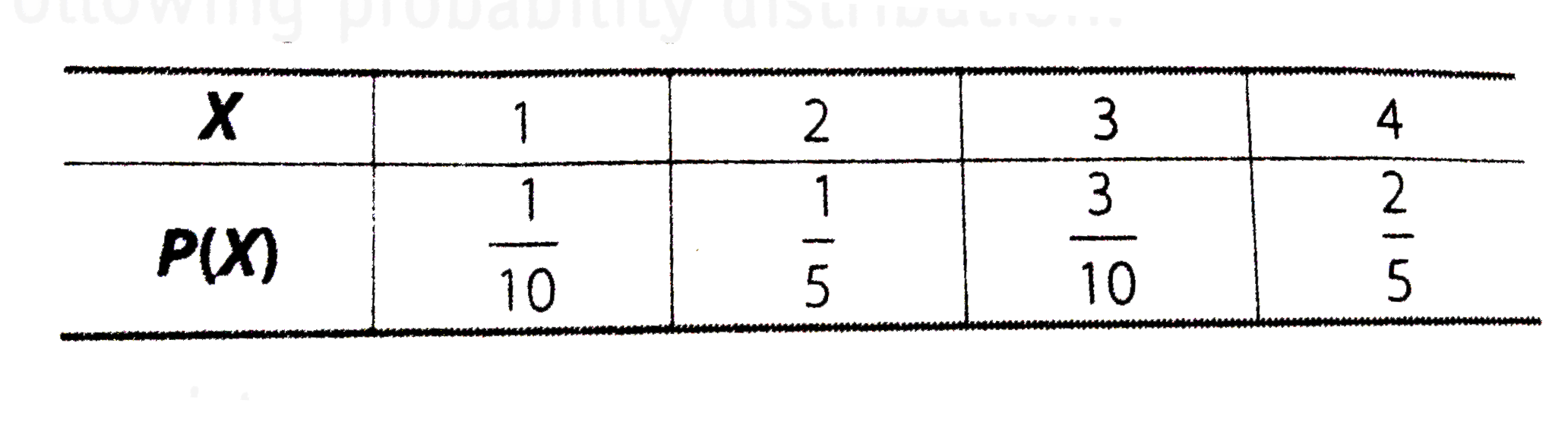
E(X2) is equal to
3
5
7
10
E(X2)=ΣX2P(X)=1⋅110+4⋅15+9⋅310+16⋅25
=110+45+2710+325
=1+8+27+6410=10
Topper's Solved these Questions
- PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - True/False
9 Videos
- PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Long Answer Type Questions
15 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
- RELATIONS AND FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Fillers
15 Videos
Similar Questions
For the following probability distribution.
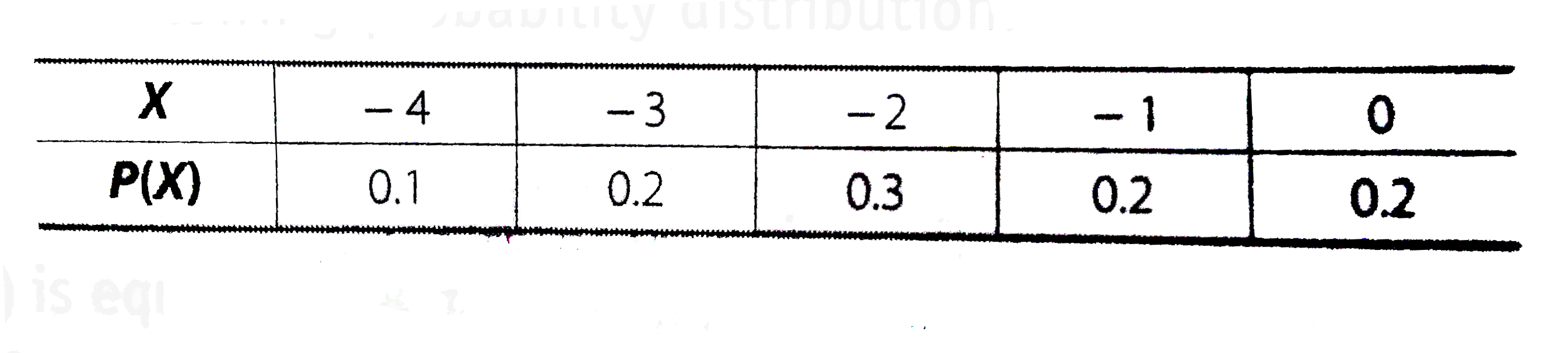
E(X) is equal to
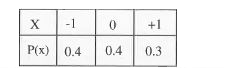
View SolutionState whether the following probability distribution is admissible or not.
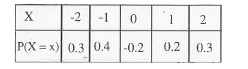
View SolutionState whether the following probability distribution is admissible or not.
View SolutionFor the following probability distribution: X: 1 2 3 4 P(X):110 15 310 25 The value of E(X2) is 3 b. 5 c. 7 d. 10
View SolutionFind the mean μ and variance σ2 for the following probability distribution :
X: 0 1 2 3
P(X): 164 1864 1864 2764
View SolutionFor the following probability distribution determine standard deviation of the random variable X.
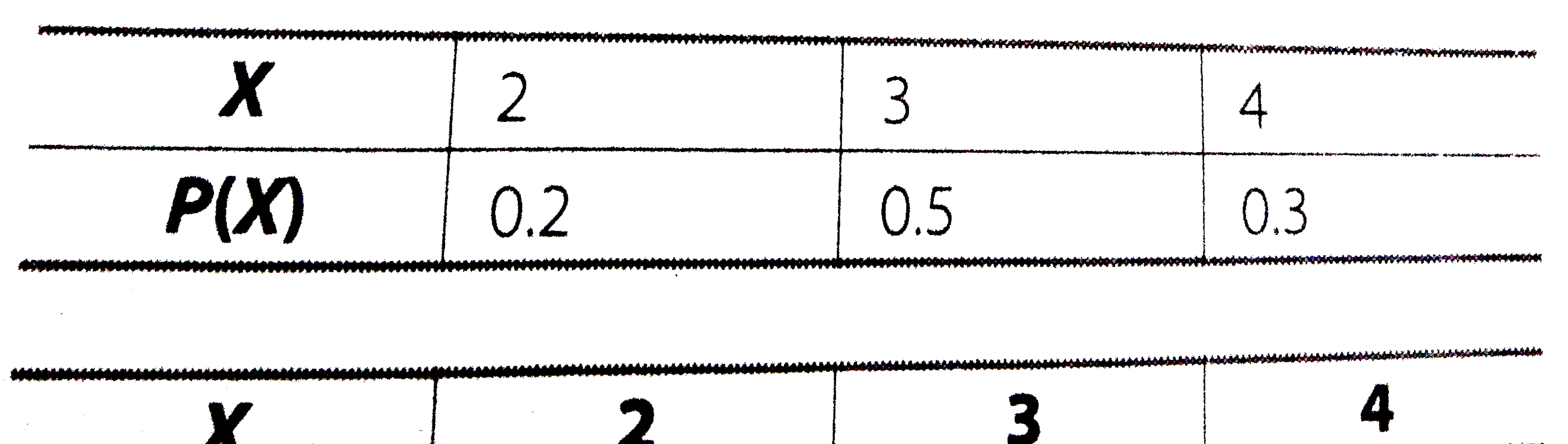
View SolutionFor the following probability distribution:
X: −4 −3 −2 −1 0
P(X): 0.1 0.2 0.3 0.2 0.2
The value of E(X) is
a .0
b. −1
c. −2
d. −1.8
View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View SolutionA random variable X has the following probability distribution :

determine the value of a
View SolutionA random variable has the following probability distribution: 1 2 3 4 5 6 7 8 For the events E=[X:X is a prime number], F={X:X<4} , the probability P(E∪F) is 0.50 b. 0.77 c. 0.35 d. 0.87
View Solution

