For the following probability distribution.
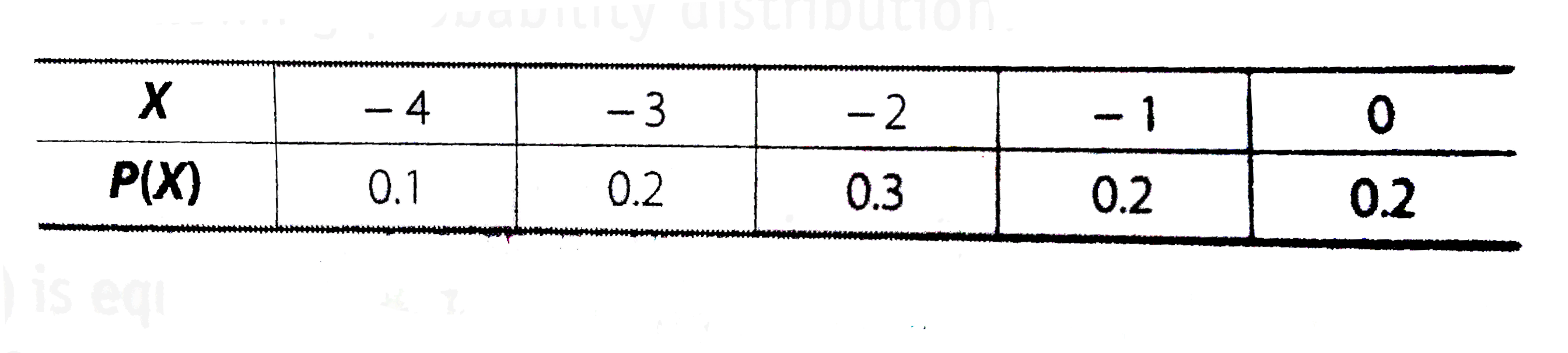
E(X) is equal to
0
−1
−2
−1.8
E(X)=ΣXP(X)
=−4×(0.1)+(−3×0.2)+(−2×0.3)+(−1×0.2)+(0×0.2)
=−0.4−0.6−0.6−0.2=−1.8
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - True/False9videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Long Answer Type Questions15videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example101videos
MATRICES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Fillers15videos
RELATIONS AND FUNCTIONS
Similar Questions
For the following probability distribution.
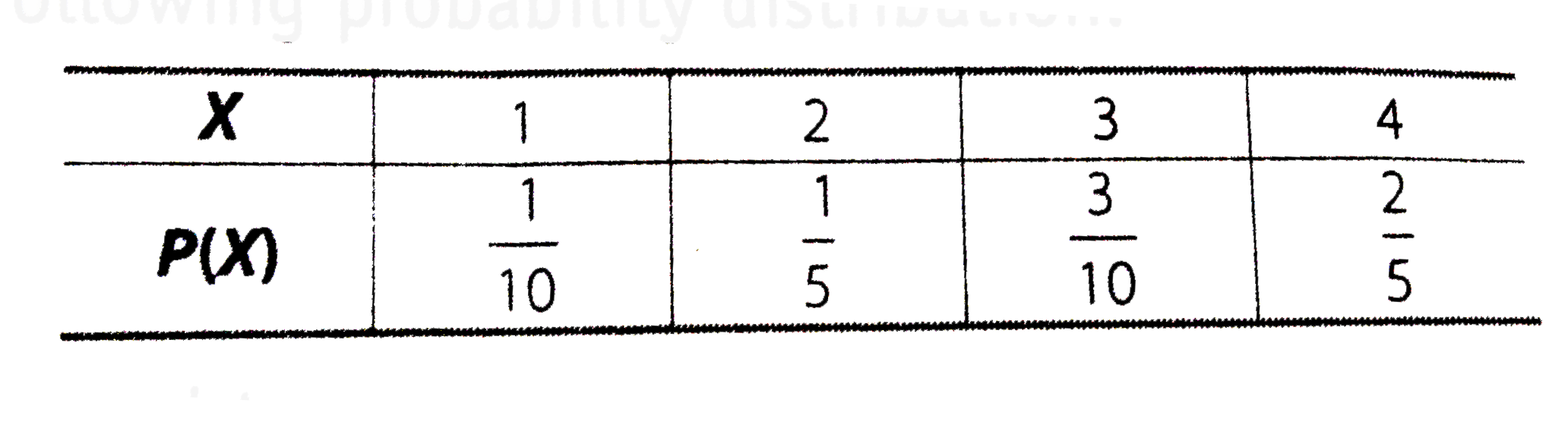
E(X2) is equal toView SolutionFor the following probability distribution :

E(X2) is equal toView SolutionFor the following probability distribution: X: 1 2 3 4 P(X):110 15 310 25 The value of E(X2) is 3 b. 5 c. 7 d. 10
View SolutionFor the following probability distribution:
X: −4 −3 −2 −1 0
P(X): 0.1 0.2 0.3 0.2 0.2
The value of E(X) is
a .0
b. −1
c. −2
d. −1.8View SolutionState whether the following probability distribution is admissible or not.
 View Solution
View SolutionState whether the following probability distribution is admissible or not.
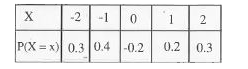 View Solution
View SolutionFind the mean variance and standard deviation of the following probability distribution xi:a b pi:p q Where p+q=1.
View SolutionA random variable X has the following probability distribution :

determine the value of a
View SolutionFor the following probability distribution determine standard deviation of the random variable X.
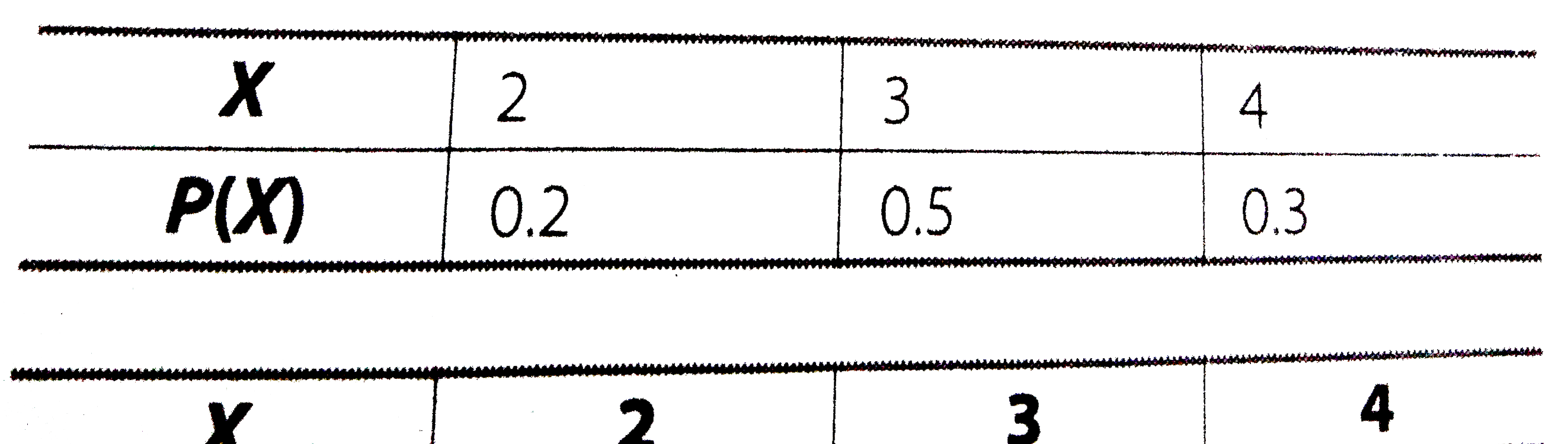 View Solution
View SolutionA random variable has the following probability distribution: 1 2 3 4 5 6 7 8 For the events E=[X:X is a prime number], F={X:X<4} , the probability P(E∪F) is 0.50 b. 0.77 c. 0.35 d. 0.87
View Solution

