Find the mean, variance, standard deviation of number 6 in the two throws of a dice.
In a single tosses, we have
probability of getting a six =16, and probability of getting a non-six =(1−16)=56.
Let X denote the number of sixes in two tosses.
Then, clearly X can assume the value 0, 1, or 2.
P(X=0)=P(non-six in the 1st draw) and (non-six in the 2nd draw)]
=P(non-six in the 1st draw) ×P(non-six in the 2nd draw)
=(56×56)=2536.
P(X=1)=P[six in the 1st draw and non-six in the 2nd draw) or (non-six in the 1st draw and six in the 2nd draw)]
=P(six in the 1st draw and non-six in the 2nd draw)
+P (non-six in the 1st draw and six in the 2nd draw)
=(16×56)+(56×16)=(536+536)=1036=518.
P(X=2)=P[six in the 1st draw and six in the 2nd draw]
P=(six in the 1st draw) × P (six in the 2nd draw)
=(16×16)=136.
Hence, the probability distribution is given by

∴ mean,μ=Σxipi=(0×2536)+(1×518)+(2×136)=618=13.
Variance, σ2=Σx2ipi−μ2
=[(0×2536)+(1×518)+(4×136)−19]=518.
Standard deviation, σ=√518=13⋅√52.
Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONBook:RS AGGARWALChapter:PROBABILITY DISTRIBUTIONExercise:Exercise 31
Explore 18 Videos
- PROBABILITY DISTRIBUTIONBook:RS AGGARWALChapter:PROBABILITY DISTRIBUTIONExercise:Objective Questions
Explore 30 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Exercise 29 B
Explore 2 Videos
- PRODUCT OF THREE VECTORSBook:RS AGGARWALChapter:PRODUCT OF THREE VECTORSExercise:Objective Questions
Explore 34 Videos
Similar Questions
Find the mean, variance and standard deviation of the number of tails in two tosses of a coin.
View SolutionFind the mean, variance and standard deviation of the number heads when three coins are tossed.
View SolutionFind the mean, variance and standard deviation using short-cut method
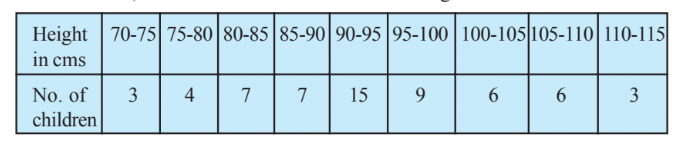
View SolutionFind the mean variance and standard deviation using short-cut method

View SolutionFind the mean, variance and standard deviation using short-cut method.
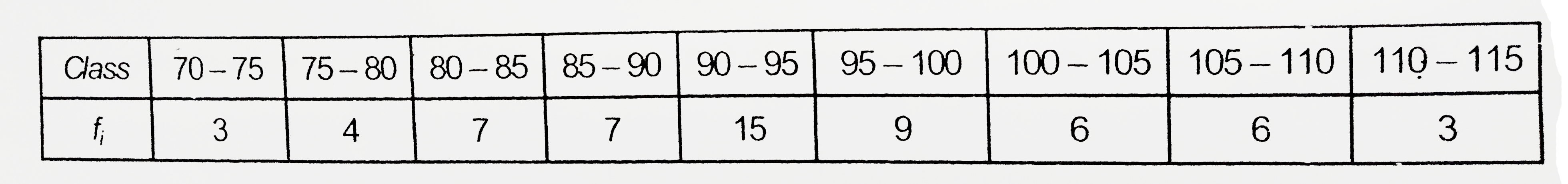
View SolutionFind the mean, variance and standard deviation of first n natural numbers.
View SolutionDetermine variance and standard deviation of the number of heads in three tosses of a coin.
View SolutionFind the variance and standard deviation for the following data:
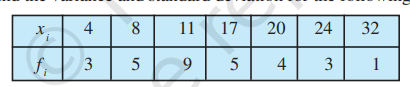
View SolutionFind the mean, variance and standard deviation for the numbers 4, 6, 10, 12, 7, 8, 13, 12.
View SolutionTwo cards are drawn simultaneously (or successively without replacement) from a well shuffled pack of 52 cards. Find the mean, variance and standard deviation of the number of kings.
View Solution
