Equation of a circle which passes through (3,6) and touches the axes is
A
x2+y2+6x+6y+3=0
B
x2+y2−6x−6y−9=0
C
x2+y2−6x−6y+9=0
D
none of these
Video Solution
Text Solution
The correct Answer is:C
Let centre of the circle be (a,a), then equation of the circle is (x−a)2+(y−a)2=a2
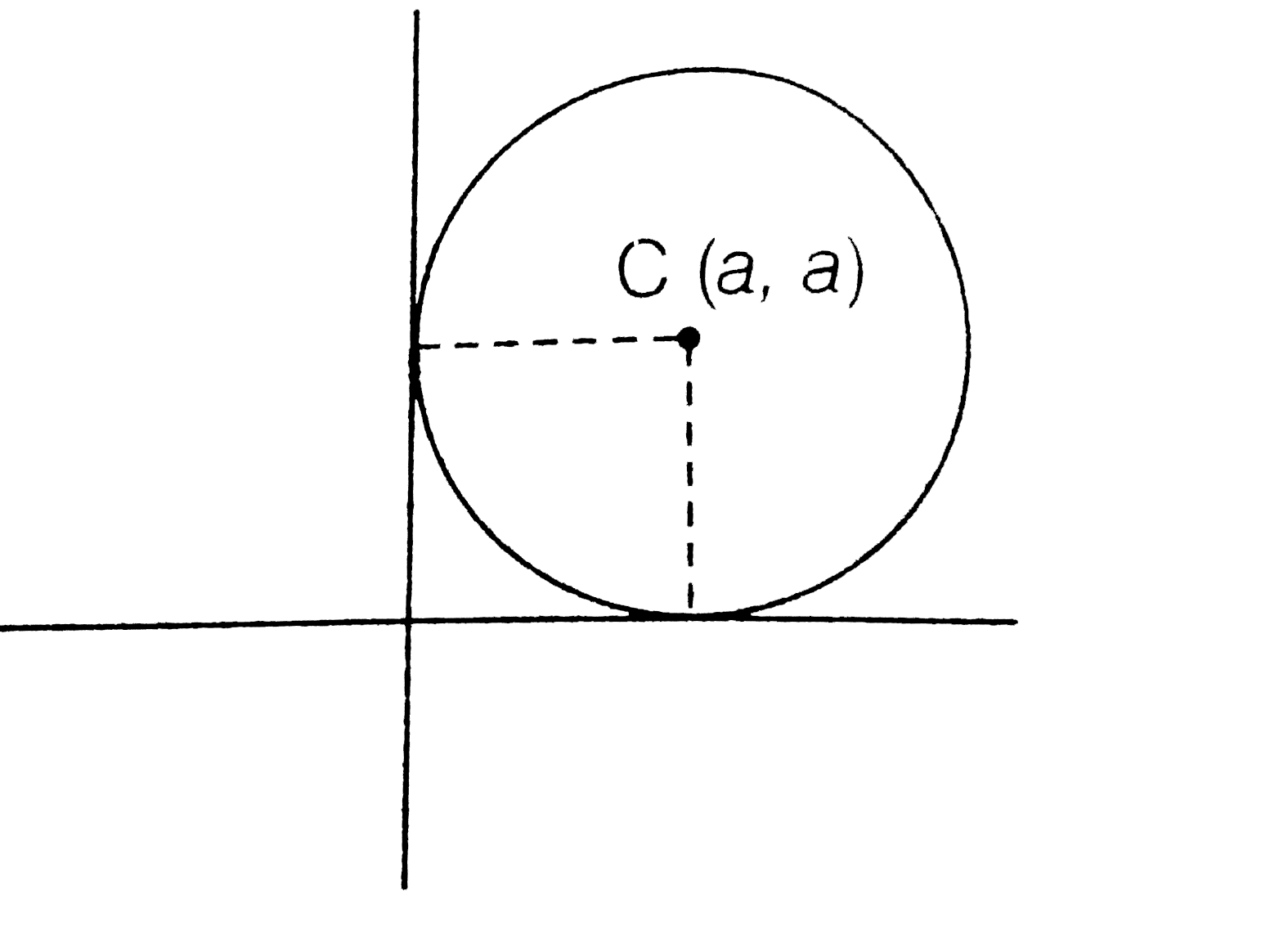
Since, the point (3,6) lies on the circle then
(3−a)2+(6−a)2=a2
⇒a2+9−6a+36−12a+a2=a2
⇒a2−15a−3a+45=0
⇒a2−15a−3a+45=0
⇒a(a−15)−3(a−15)=0
⇒(a−3)(a−15)=0
⇒a=3,a=15
So, the equation of the circle is
(x−3)2+(y−3)2=9
⇒x2−6x+9+y2−6y+9=9
⇒x2+y2−6x−6y+9=0
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - CONIC SECTIONSEXERCISE - Fillers6videos
CONIC SECTIONS
- BOOK - NCERT EXEMPLARCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - OBJECTIVE TYPE QUESTIONS16videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - NCERT EXEMPLARCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - Fillers16videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
Equation of circle which passes through (-1,2) and
(1,2) , and touches the line y = 5 , isA9x2+9y2−60y+75=0B9x2+9y2−60−75=0C9x2+9y2+60y−75=0D9x2+9y2+60+75=0 - Question 2 - Select One or More
The equation of a circle passing through (3,6) touching both the axes is
Ax2+y2−6x−6y+9=0Bx2+y2+6x−6y+9=0Cx2+y2+30x−30y+225=0Dx2+y2−30x−30y+225=0 - Question 3 - Select One or More
The equation of circle passing through (-1,-2) and touching both the axes is
Ax2+y2−2x−2y−1=0Bx2+y2+2x+2y+1=0Cx2+y2+10x+10y+25=0Dx2+y2−2x−2y+1=0
Equation of a circle passing through 3 points
View SolutionFind the equations of circles which passes through thepoint (-4.-2) and touches both the co-ordinate axes.
View SolutionThe equation of circles passing through (3,−6) touching both the axes is
View SolutionA is a point (a, b) in the first quadrant. If the two circIes which passes through A and touches the coordinate axes cut at right angles then :
View SolutionThe length of the diameter of the circle which passes through the point (2,3) and touches the x-axis at the point (1,0) is
View Solution
