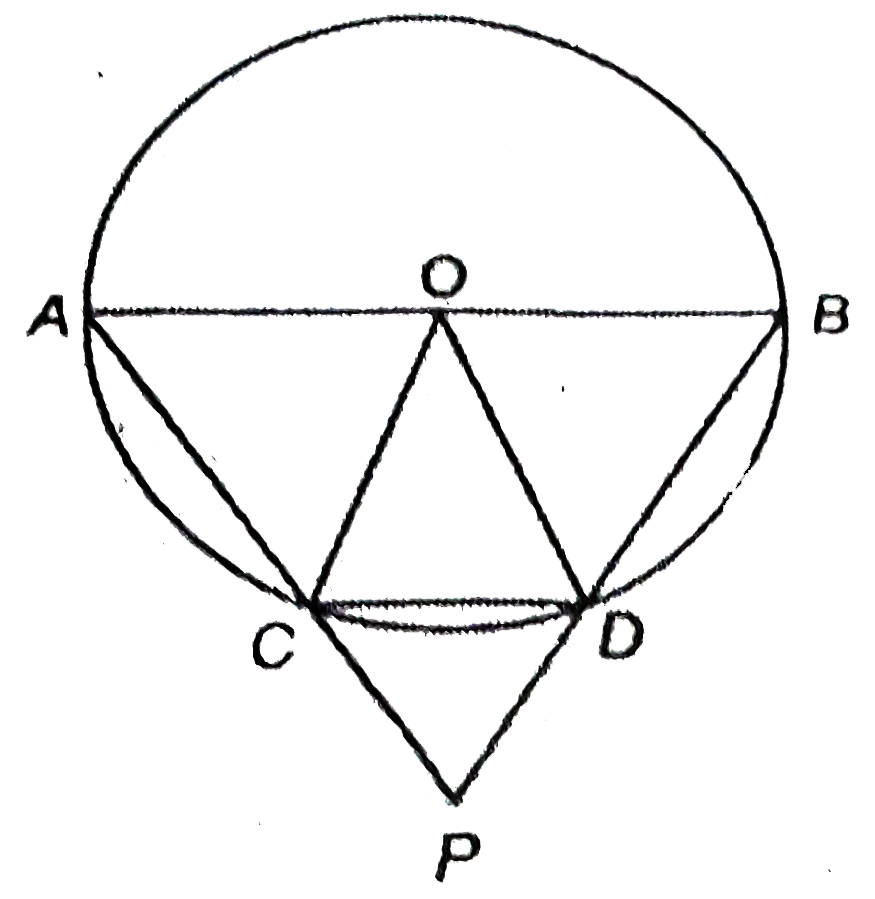
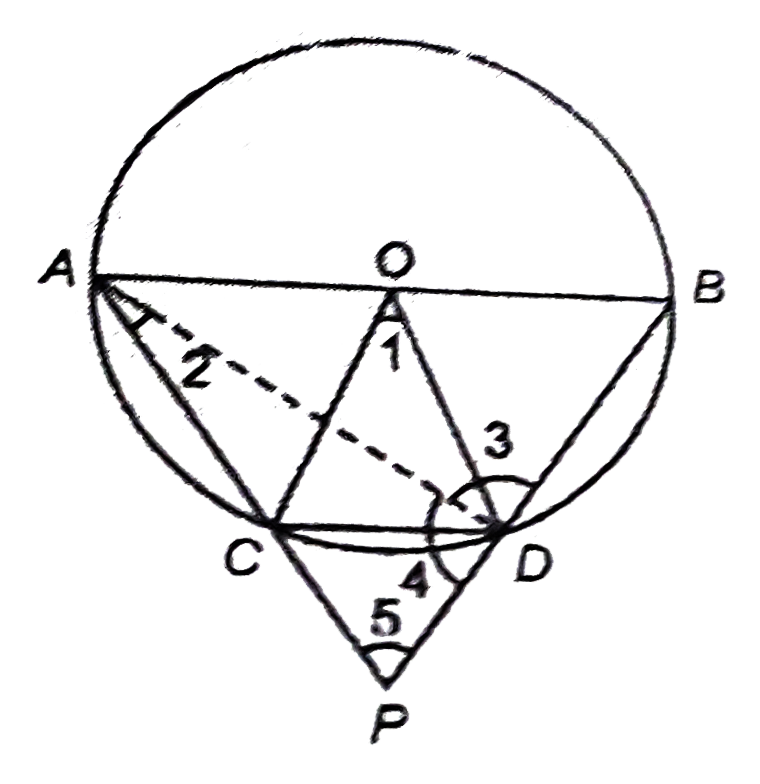
AB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
60∘
30∘
90∘
160∘
The correct Answer is:A
Since, chord CD is equal to radius
∴DC=OC=OD
⇒∠1=60∘ (∵ each angle of an equilateral triangle is of 60∘)
∴∠212∠1 (degree measure theorem)
=12×60∘=30∘ ........(1)
Now, since ∠3=90∘ (angle in a semicircle is 90∘)
⇒∠4=90∘ (linear pair axiom).....(2)
In ΔADP,
∠2+∠4+an≤5=180∘ (angle sum property)
⇒30∘+90∘+∠5=180∘
⇒∠5=180∘−120∘
60∘
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a22videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b19videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
Similar Questions
In the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.
 View Solution
View SolutionIn Figure, AB is a diameter of a circle C(O, r). Chord CD is equal to radius OC. If AC and BD when produced intersect at P, prove that ∠APB is constant.
View Solution
Knowledge Check
- Question 1 - Select One
AB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
A120∘B30∘C60∘D90∘ - Question 2 - Select One
AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
A30∘B60∘C90∘D45∘ - Question 3 - Select One
AB is a diameter of the circle with centre O, CD is chord of the circle. If ∠BOC=120∘, then the value of ∠ADC is
A42∘B30∘C60∘D35∘
AB is diameter of a circle with centre 'O'. CD is a chord which is equal to the radius of the circle. AC and BD are extended so that they intersect each other at point P. Then find the value of ∠APB.
View SolutionIn the adjoining figure,AB is the diameter of the circle of centre O & the chord CD is equal to radius. If P is an external point, then find the value of ∠APB.
View SolutionIn Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to theradius of the circle. AC and BD when extended intersect at a point E. Prove that∠AEB = 60∘
View SolutionIn the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
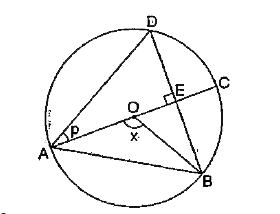 View Solution
View SolutionAB is a chord in a circle with centre O. AB is produced to C such that BC is equal to the radius of the circle. C is joined to O and produced to meet the circle at D. If ∠ACD=32∘, then the measure of ∠AOD is .......
View Solution
