A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
21.4m
20.4m
30.4m
40.4m
The correct Answer is:B
Let BC=18 m be the flag pole and its shadow be AB=9.6 m. The distance of the top of the pole, C from the far end i.e., A of the shadow is AC.
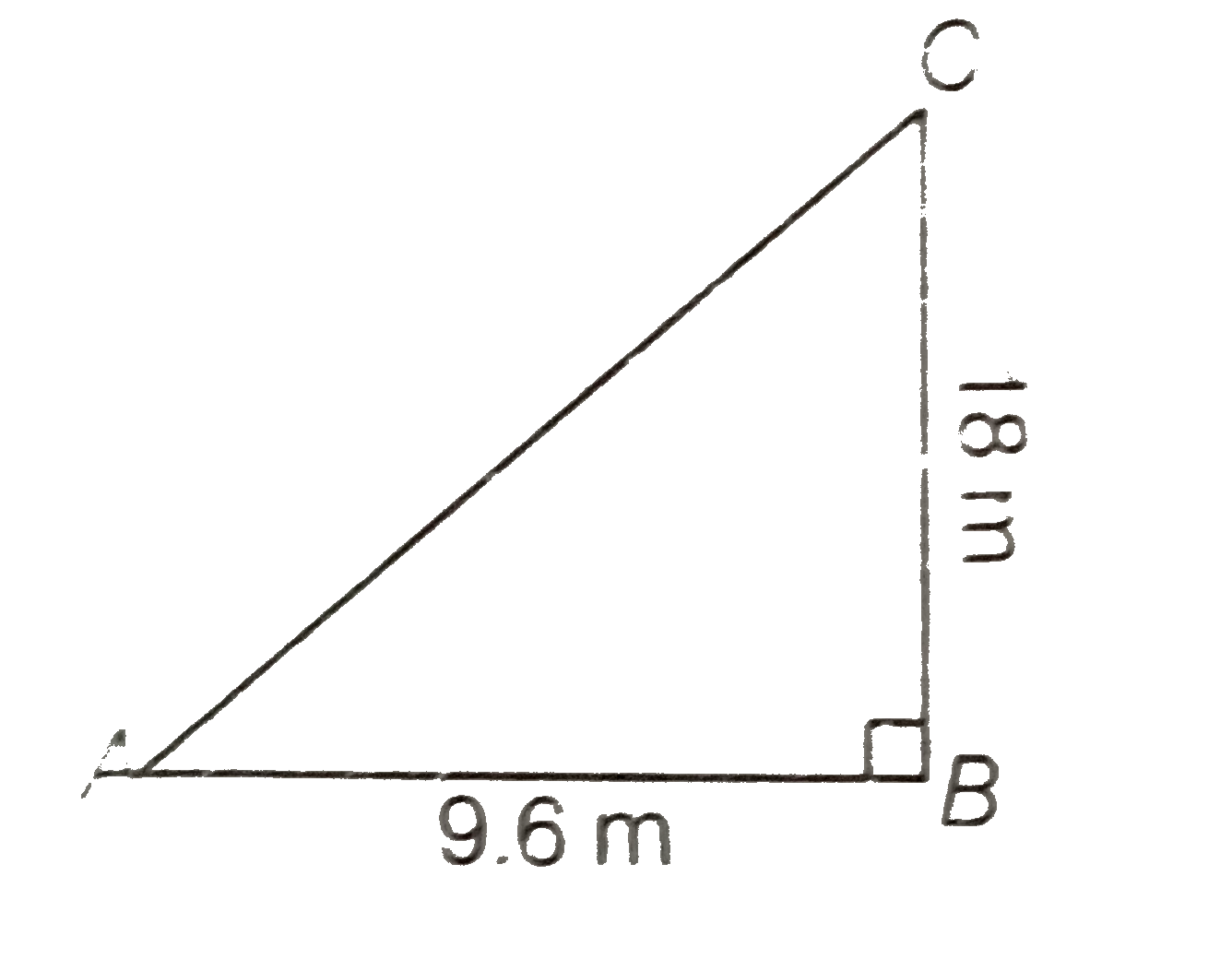
In right angled ΔABC, AC2=AB2+BC2 [by Pythagoras theorem]
⇒AC2=(9.6)2+(18)2
AC2=92.16+324
⇒AC2=416.16
∴AC=√416.16=20.4cm
Hence, the required distance is 20.4 m.
Topper's Solved these Questions
Similar Questions
A pole 6 m high casts a shadow 2 3 m long on the ground, then find the angle oi elevation of the sun.
View SolutionA vertical pole 5 m 60 cm high casts a shadow 3 m 20 cm long. Find at the same time (i) the length of shadown cast by another pole 10 m 50 cm high.
(ii) the height of a pole which casts a shadow 5 m long.View Solution
Knowledge Check
- Question 1 - Select One
At a particular time , the shadow cast by a tower is 6 m long. If the distance from the top of the tower to the end of the shadow is 10 m long, determine the height of the tower.
A4 mB8 mC16 mD12 m - Question 2 - Select One
If a pole 12 m high casts a shadow 4√3m long on the ground then the sun's elevation is
A60∘B45∘C30∘D90∘ - Question 3 - Select One
A pole 14 m high casts a shadow of 10 m. At the same time , what will be the height of a tree, the length of whose shadow is 7 meters?
A20mB9.8mC5mDnon of these
If a tower 30 m high, casts a shadow 10√3 m long on the ground, then what is the angle of elevation of the sun ?
View SolutionIf a tower 30 m high, casts a shadow 10√3m long on the ground, then what is the angle of elevation of the sun ?
View SolutionA pole of height 6 m casts a shadow 2√3 m long on the ground. Find the sun's elevation.
View SolutionA vertical stick 1.8 m long casts a shadow 45 cm long on the ground. At the same time, what is the length or the shadow of a pole 6 m high?
View SolutionIf a pole of 12 m height casts a shadow of 4√3 m long on the ground , then the sun 's angle of elevation at that instant is
View Solution
