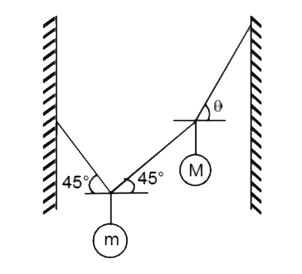
Two bodies of masses m and 4m are attached to a light string as shown in figure. A body of mass m hanging from string is executing oscillations with angular amplitude 60∘, while other body is at rest on a horizontal surface. The minimum coefficient of friction between mass 4m and the horizontal surface is (here pulley is light and smooth)

A
(a) 14
B
(b) 34
C
(c) 12
D
(d) 18
Video Solution
Text Solution
The correct Answer is:C
Velocity at lowest position =√2gl(1−cos60∘)=√gl
T=mg+mV2l=mg+mlgl=2mg
∴T=μ4mg⇒12
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective23videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Practice Problems
- Question 1 - Select One
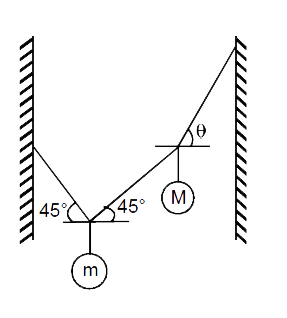
Two bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass m hanging from a string of length l is executing oscillations of angular amplitude θ0 while the other body is at rest. The minimum coefficient of friction between the mass 4m and the horizontal surface should be
 A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04)
A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04) - Question 1 - Select One
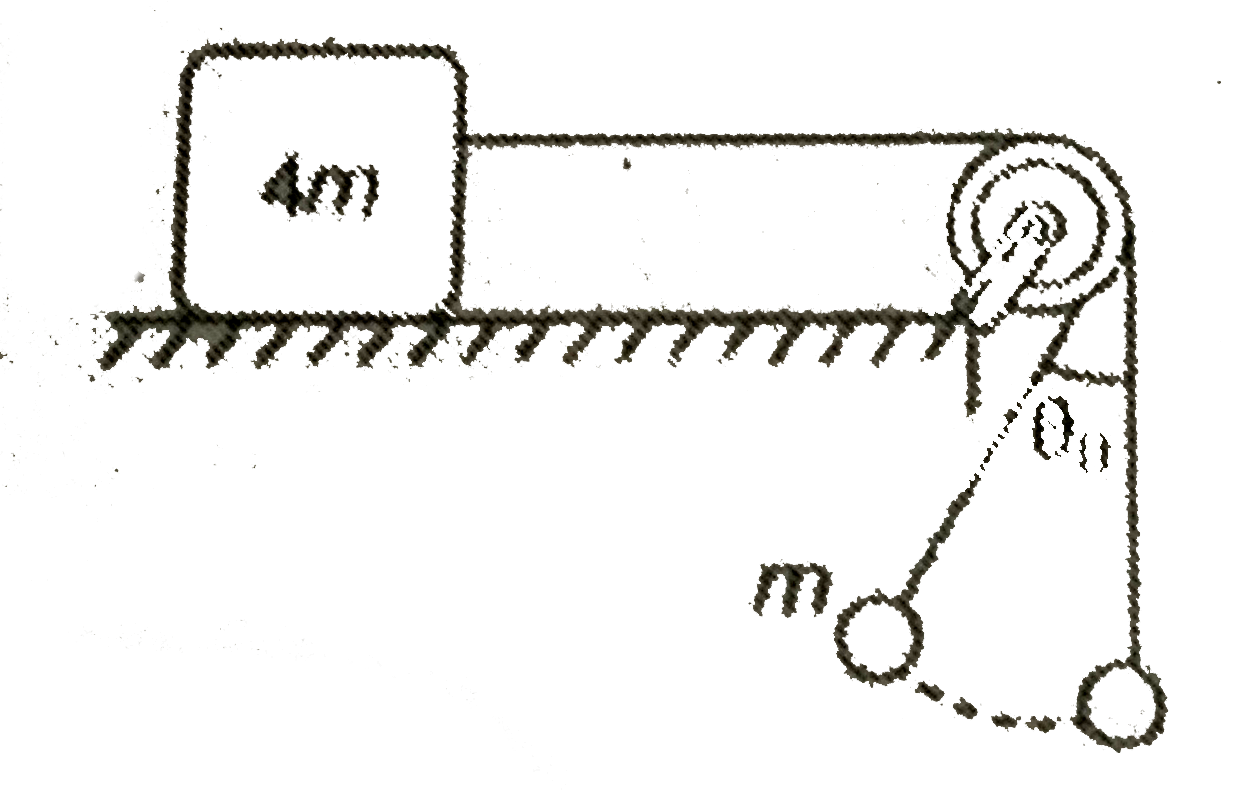
Two bodies of mass m and 4m are attached by a string shown in the figure-2.146. The body of mass m hanging from a string of length l is executing simple harmonic motion with amplitude A while other body is at rest on the surface. The minimum coefficient of friction between the mass 4m and the horizontal surface must be to keep it at rest is :
 A14(1−A2l2)B14(1+A2l2)C14AlcosθD14
A14(1−A2l2)B14(1+A2l2)C14AlcosθD14 - Question 1 - Select One
Two bodies of mass m and 4m are attached with string of length l is excurting oscillations of angular amplitude θ0 while the other body is at rest . The minimum coefficient of friction between the mass 4m and the horizontal surface should be:
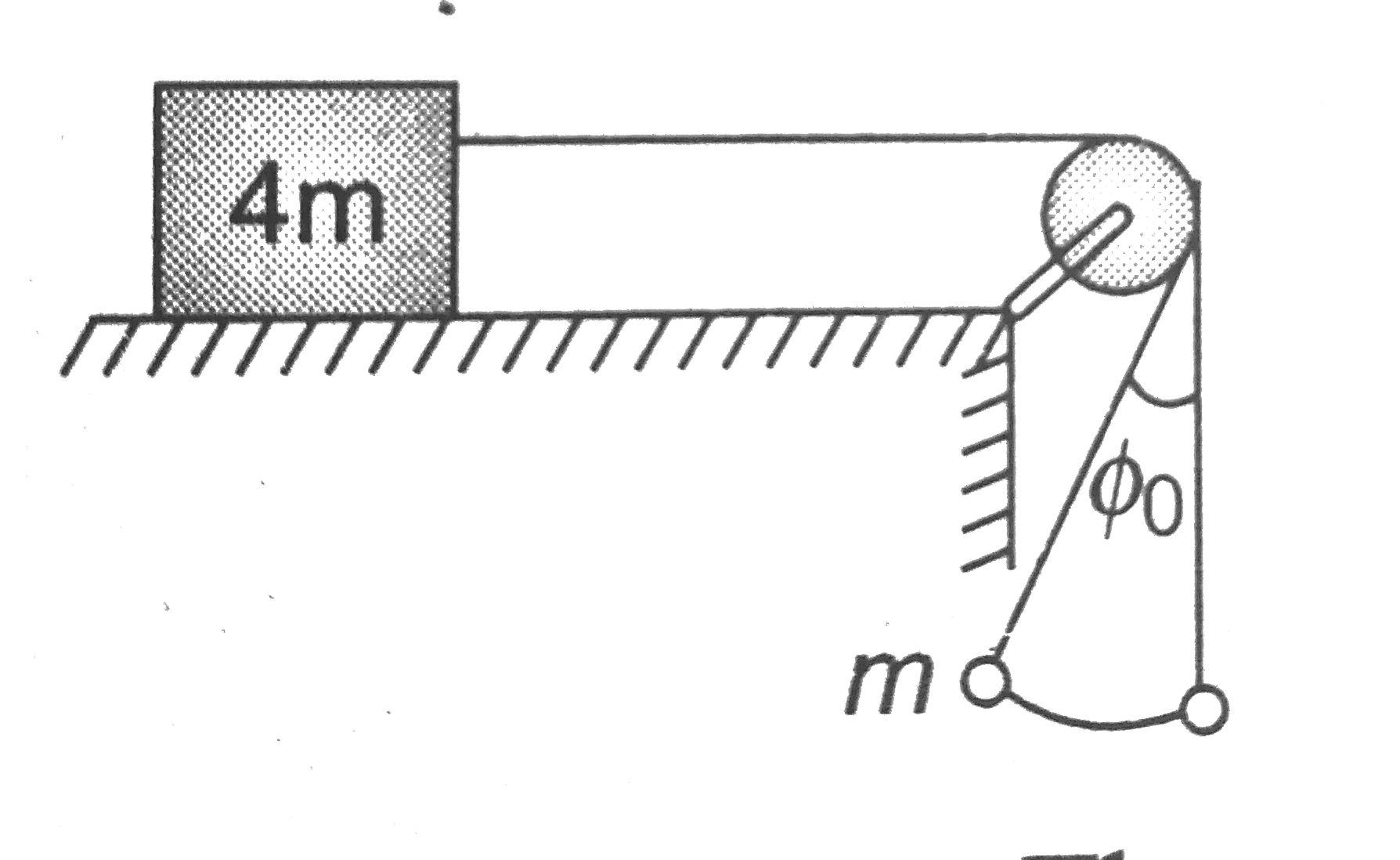 A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−cosθ04)
A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−cosθ04) - Question 1 - Select One
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
 Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mM
Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mM - Question 1 - Select One
A mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is μ. The force of friction between the mass and the surface is :
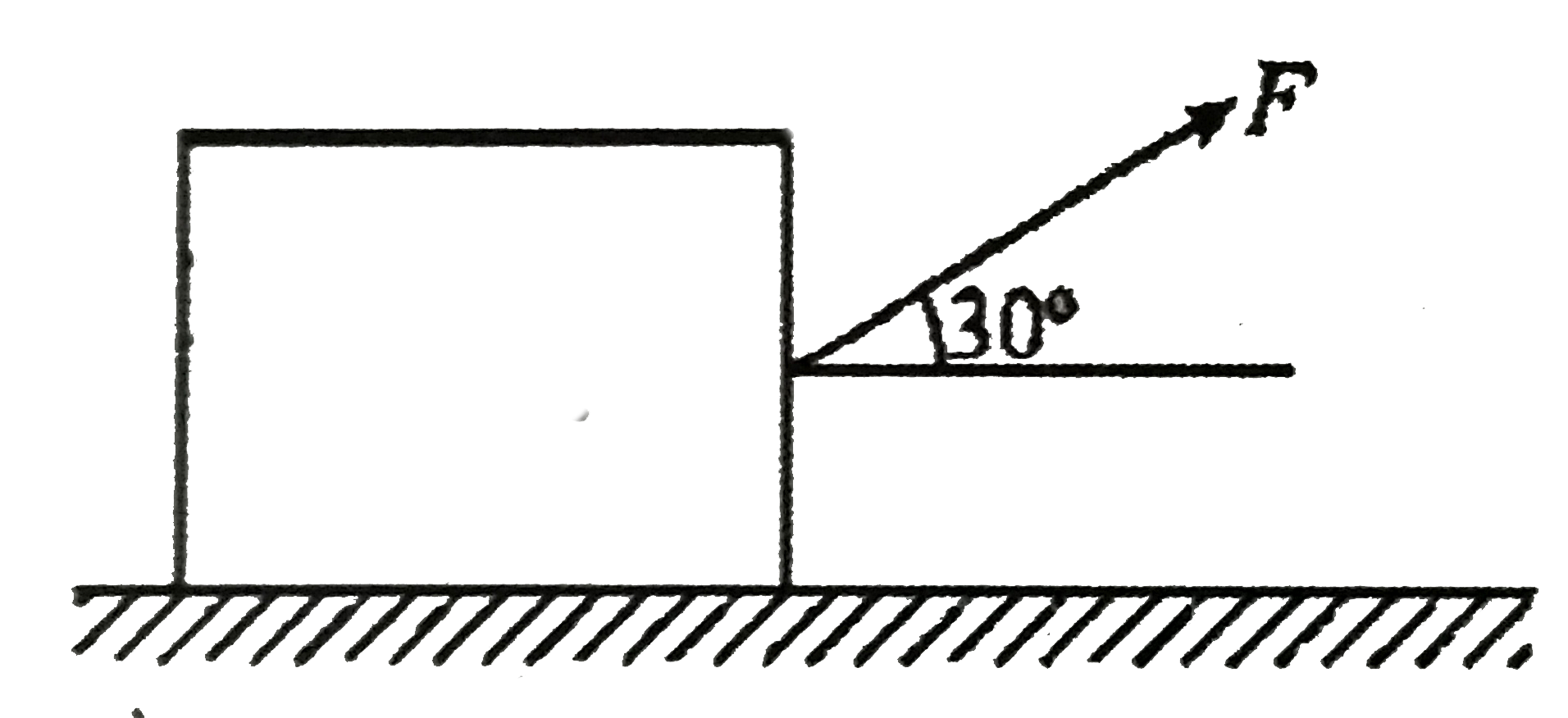 AμmgBμ[mg+F2]CF√32Dμ[mg−F2]
AμmgBμ[mg+F2]CF√32Dμ[mg−F2] - Question 1 - Select One or More
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above - Question 1 - Select One
A body of mass m, having momentum p, is moving on a rough horizontal surface. If it is stopped in a distance x, the coefficient of friction between the body and the surface is given by
Aμ=p22gm2xBμ=p22mgxCμ=p2mgxDμ=p2gm2x - Question 1 - Select One or More
Two masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g