Three travelling waves are superimposed. The equations of the wave are
y!=A0sin(kx−ωt),y2=3√2A0sin(kx−ωt+ϕ) and y3=4A0cos(kx−ωt)
find the value of ϕ(given 0≤ϕ≤π/2) if the phase difference between the resultant wave and first wave is π/4
π6
π3
π12
None of these
The correct Answer is:C
Given, y1=A0sin(kx−ωt)
y2=3√2A0sin(kx−ωt+ϕ),
and y3=4A0cos(kx−ωt),
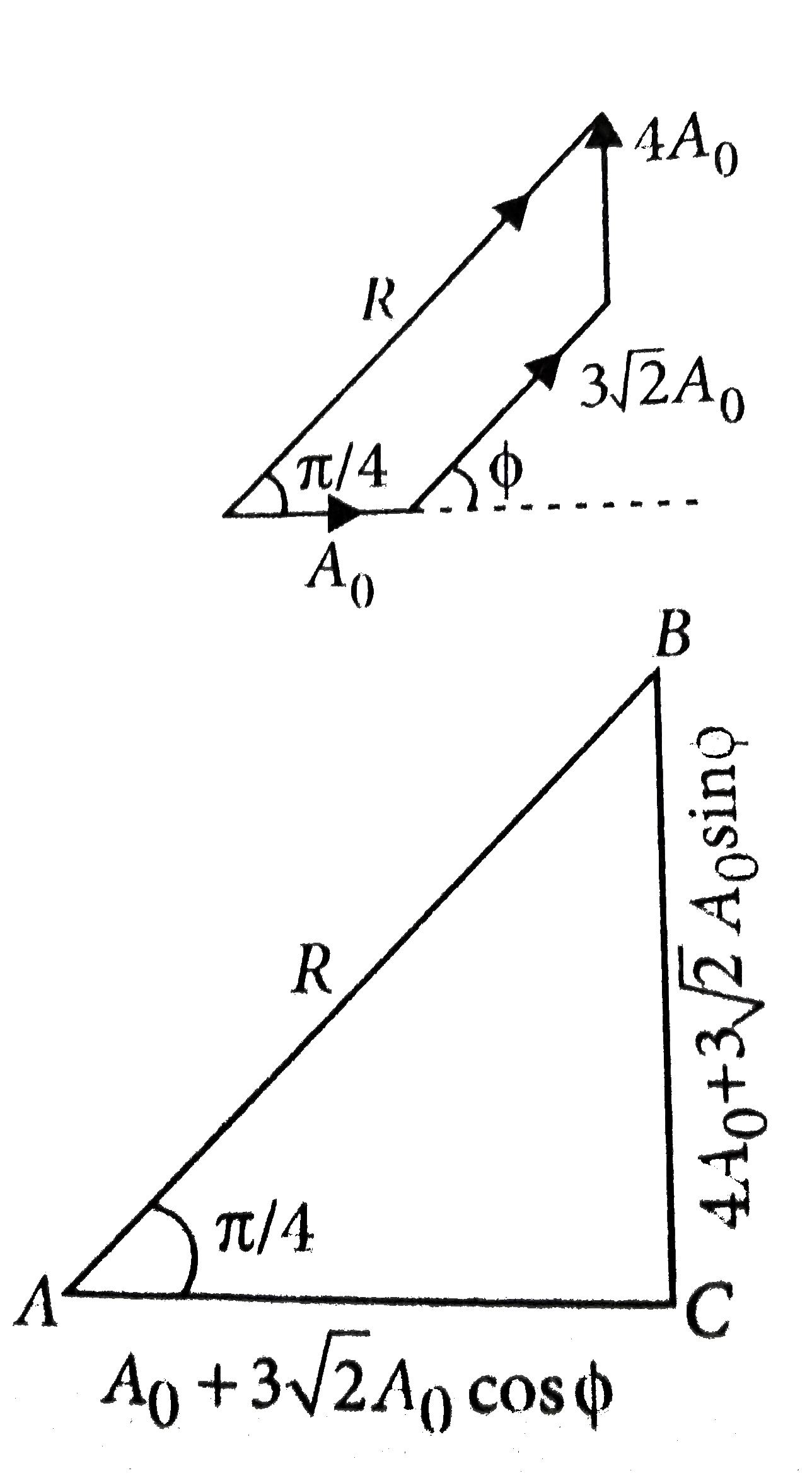
These waves can be represented by phase diagram as shown.
From phase diagram,
tan(π4)=BCAC=A0(4+3√2sinϕ)A0(1+3√2cosϕ)
⇒ 4+3√2sinϕ=1+3√2cosϕ
⇒ cosϕ−sinϕ=1√2
Squaring both sides, we get
cos2ϕ+sin2ϕ−2sinϕcosϕ=12
1−2sinϕcosϕ=12 or 2ϕ=π6⇒ϕ=π12
Related Playlists
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - EXEMPLER10videos
WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - ASSERTION15videos
WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason15videos
WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason15videos
UNITS AND MEASUREMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - Assertion And Reason15videos
WORK , ENERGY AND POWER
Knowledge Check
- Question 1 - Select One
if x=asin(ωt+π/6) and x'=acosω, t, then what is the phase difference between the two waves
Aπ/3Bπ/6Cπ/2Dπ - Question 1 - Select One
Two waves are represented by the equations
y1=asin(ωt+kx+0.57)m and
y2=acos(ωt+kx)m,
where x is in metres and t is in seconds. The phase difference between them isA1.0 radianB1.25 radianC1.57 radianD0.57 radian - Question 1 - Select One
A travelling wave represented by
y=Asin(ωt−kx)
is superimposed on another wave represented by
y=Asin(ωt+kx). The resultant isAstanding wave having nodes at x=(n+12)λ2, n=0,1,2,….Bsatnding wave having nodes at x=nλ2,n=0,1,2..Cwave travelling along +x directionDwave travelling along-x direction
Similar Questions
Two sinusoidal waves are superposed. Their equations are
y1=Asin(kx−ωt+π6)andy2=Asin(kx−ωt−π6)
the equation of their resultant isView SolutionLet the two waves y1=Asin(kx−ωt) and y2=Asin(kx+ωt) from a standing wave on a string . Now if an additional phase difference of ϕ is created between two waves , then
View SolutionA travelling wave in a stretched string is described by the equation y=Asin(kx−ωt) the maximum particle velocity is
View SolutionThe resultant amplitude of a vibrating particle by the superposition of the two waves
y1=asin[ωt+π3] and y2=asinωt isView SolutionAssertion: Two equations of wave are y1=Asin(ωt−kx)andy2Asin(kx−ωt). These two waves have a phase difference of π.
Reason: They are travelling in opposite directions.View SolutionThe phase difference between the waves y=acos(ωt+kx)andy=asin(ωt+kx+π2) is
View SolutionTwo waves are given by y1=asin(ωt−kx) and y2=acos(ωt−kx). The phase difference between the two waves is -
View Solution

