Figure shows a smooth curved track terminating in a smooth horizontal part. A spring of sprng constant 400 N/m is asttached at one end ot a wedge fixed rigidly with the horizontal part. A 40 g mas is released from rest at a height of 4.9 m n the curved track. Find the maximumcompression of the spring.
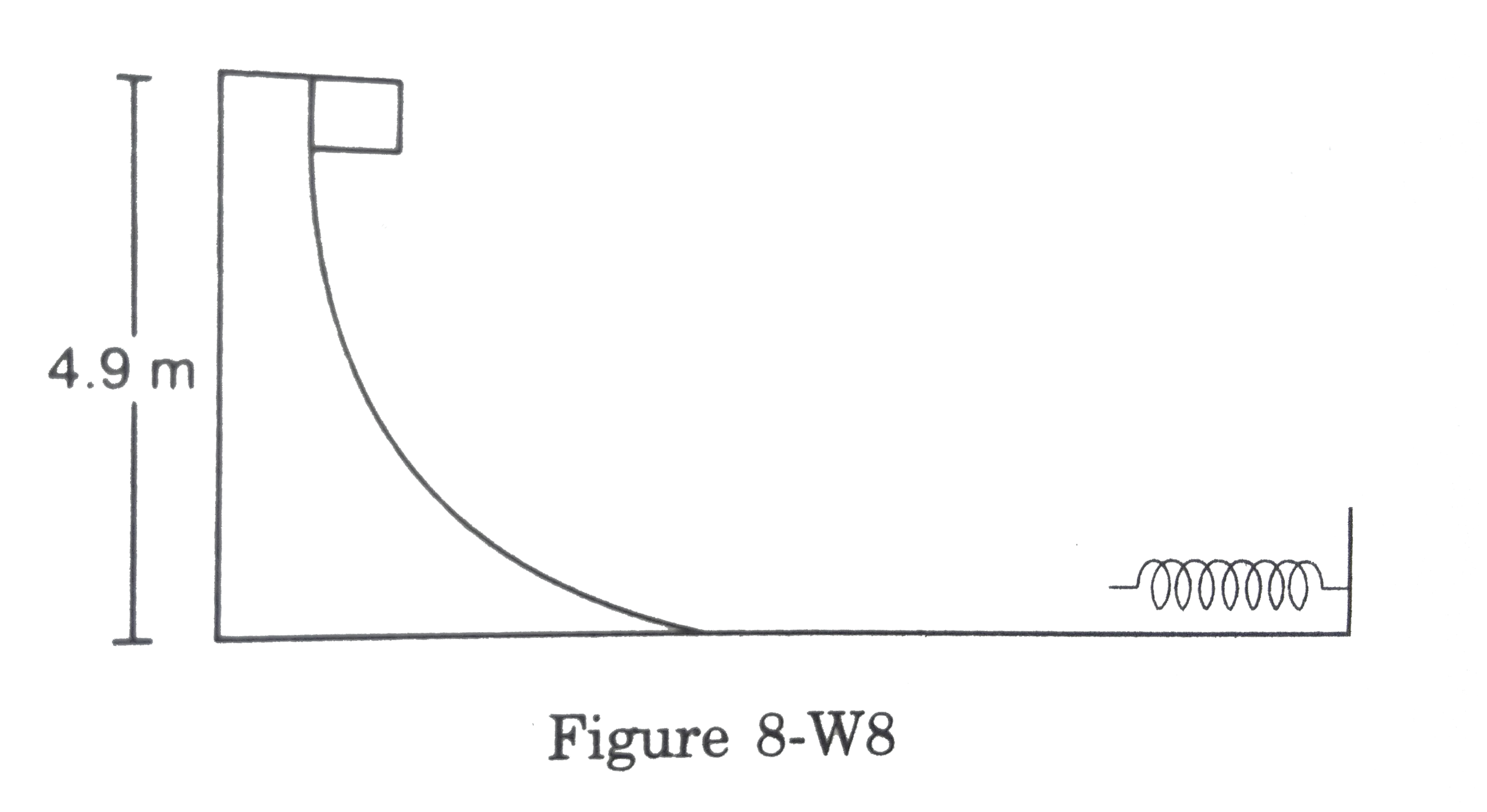
At the instant of maximum compressin the speed of the 40 g mass reduces to zero. Taking the gravitatioN/Al potential energy to be zero at the horizontal part the conservation of energy shows,
mgh=12kx2
where m=0.04 k, h=4.9 m, k=400 N/m and x is the maximum compression.
Thus, x=√2mghk
=⎛⎜
⎜⎝
⎷2×(0.04kg)×(9.8ms2)×4.9m(400Nm)
9.8cm
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Short Answer15videos
WORK AND ENERGY
- BOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Objective 110videos
WORK AND ENERGY
- BOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Exercises64videos
WORK AND ENERGY
- BOOK - HC VERMACHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises57videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
A small mass 'm' is sliding down on a smooth curved incline form a height 'h' and finally moves through a horizontal smooth surface. A light spring of force constant K is fixed with a vertical rigid stand on the horizontal surface, as shown in the figure. Find the value for the maximum compression in the spring if mass 'm' is released from rest from height 'h' and hits the spring in the horizontal surface.
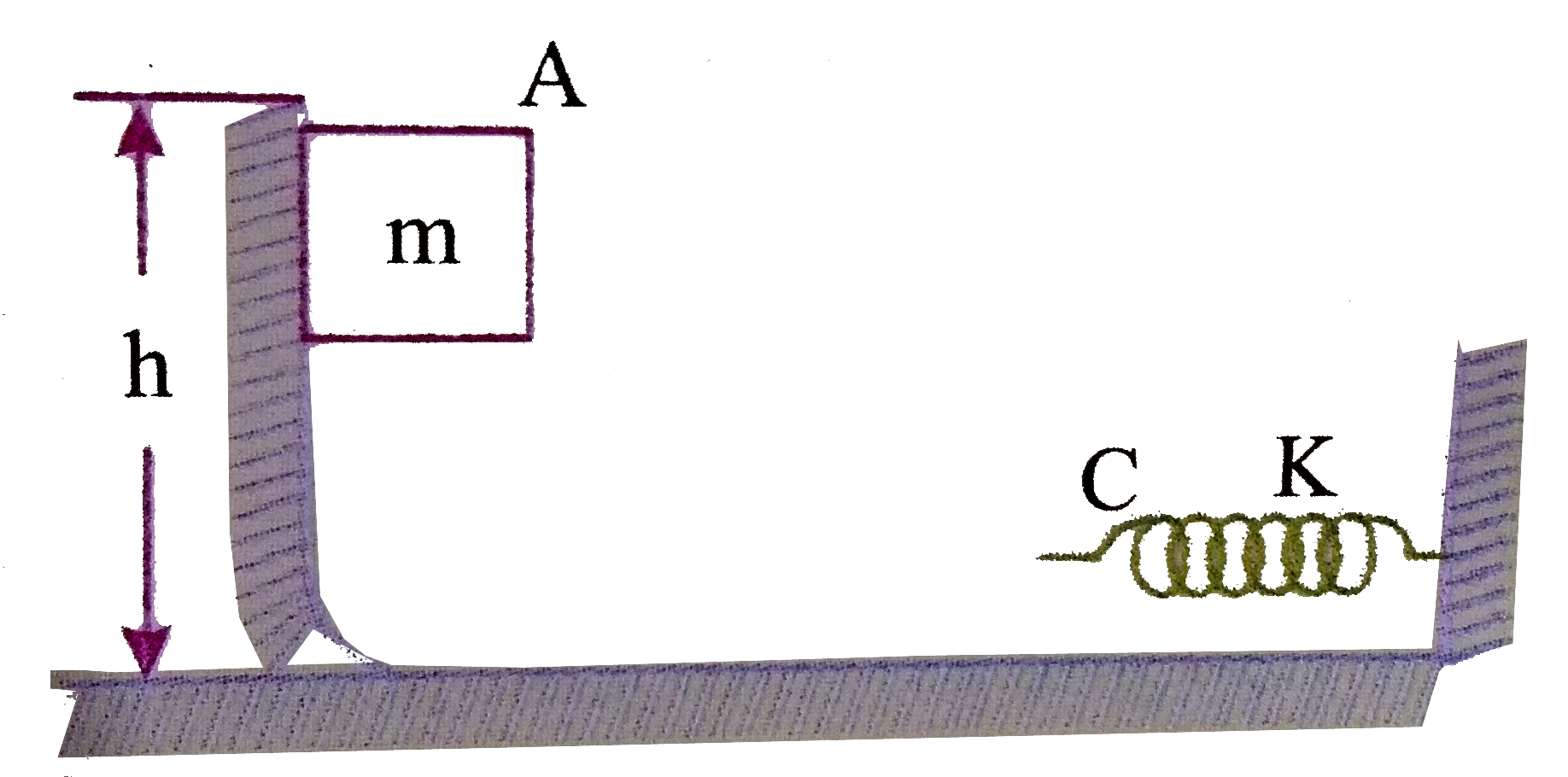 .View Solution
.View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
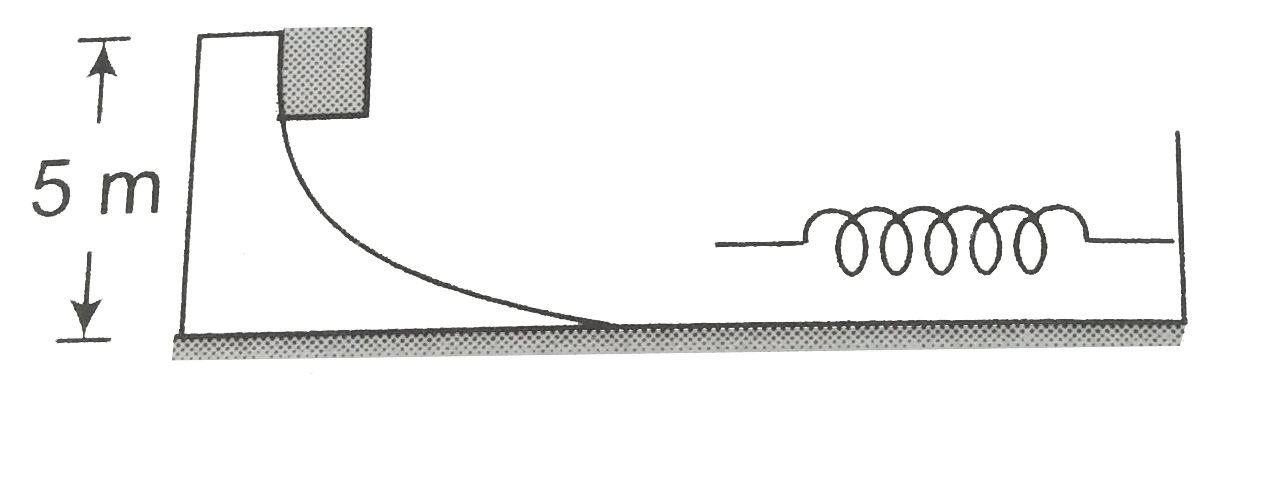
The figure shows a smooth curved track terminating in a smooth horizontal part. A spring of spring constant 400(N)/(m) is attached at one end to a wedge fixed rigidly with the horizontal part . A 40 g mass is released from rest at a height of 5 m on the curved track. The maximum compression of the spring will beA10cmB2cmC3cmD4cm - Question 2 - Select One
A smooth curved surface of height 10 m is ended horizontally. A spring of force constant 200 Nm−1 is fixed at the horizontal end as shown in figure when an object of mass 10g is released from the top, it travels along the curved path and collides with the spring. Then, the maximum compression in the spring is (Take, g=10ms−2)
A10mB0.1 cmC1 mD0.01 m - Question 3 - Select One
A block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
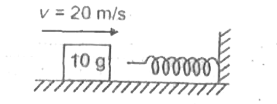 A2 mB0.2 mC20 mD43m
A2 mB0.2 mC20 mD43m
A block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View SolutionFigure shows a smooth track, a part of which is a circle of radus R. As block of mass m is pushed against a sprng of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radus of the track is horizontal.
View SolutionFigure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.
 View Solution
View SolutionThe pulley shown in figure has a radius of 20 cm and moment of inertial 0.2 kg-m^2. The string going over it is attached at one end to a vertical sprign of spring constant 50 N/m fixed from below and supports a 1 kg mas at other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has desceds through 10 cm. Take g=10ms2.
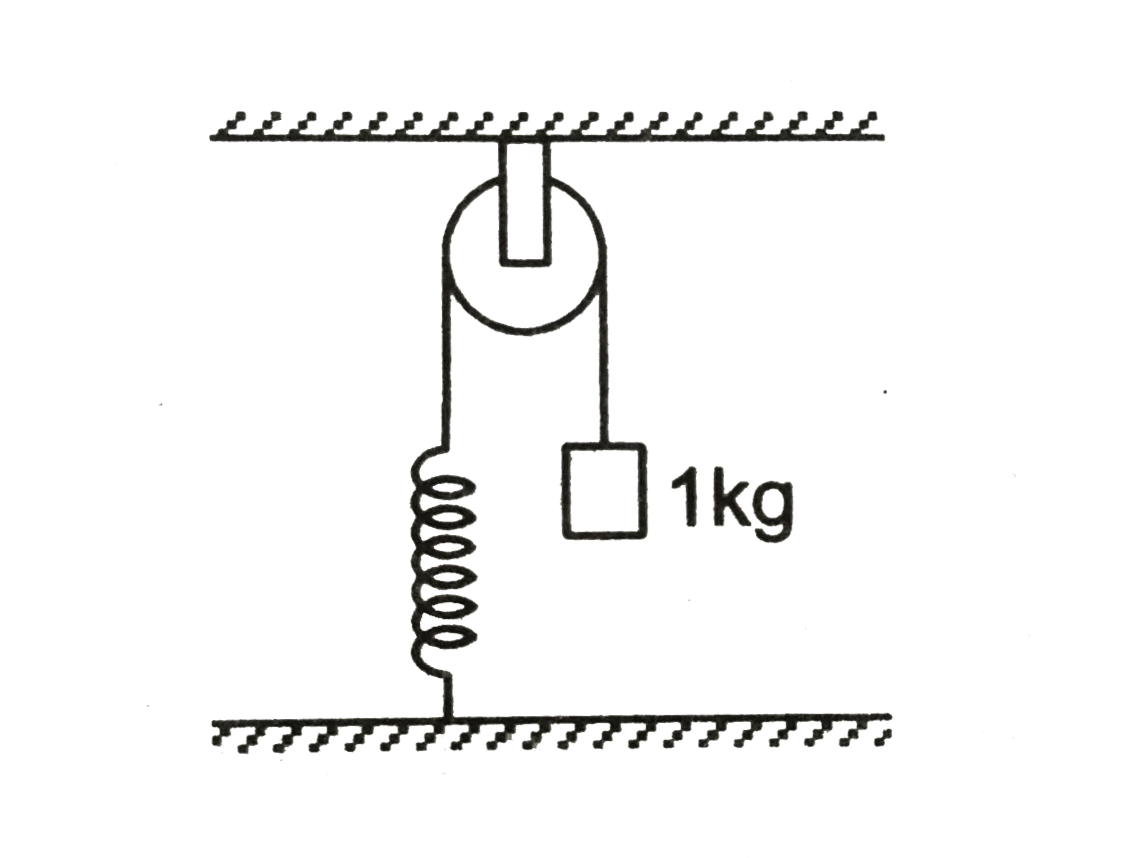 View Solution
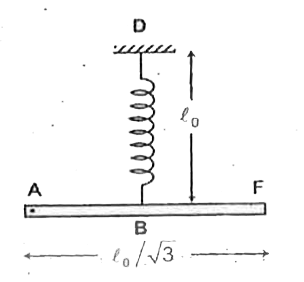
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
 View Solution
View Solution
