Consider a container having an inclined wall, inclined an angle θ with horizontal as shown in Fig. Calculate the force per unit width on the wall.

A
Fb=12ρgH2cosθ
B
Fb=12ρgH2sinθ
C
Fb=ρgH2sinθ
D
none
Video Solution
Text Solution
The correct Answer is:B
Since pressure always gets normal to the suface therefore the pressure diagram for an inclined wall is shown in Figure. The base of the triangular presure diagram is equal to ρghH because pressure at a point depends on the height of liquid column above it.

The total of application of the total force is through the centroid of the pressure diagram as shown in figure.
Alternatively the force on the inclined wall may be obtained in two parts horizontal and vertical.
The horizontal force Fx acts on the vertical projection of the inclined wall.
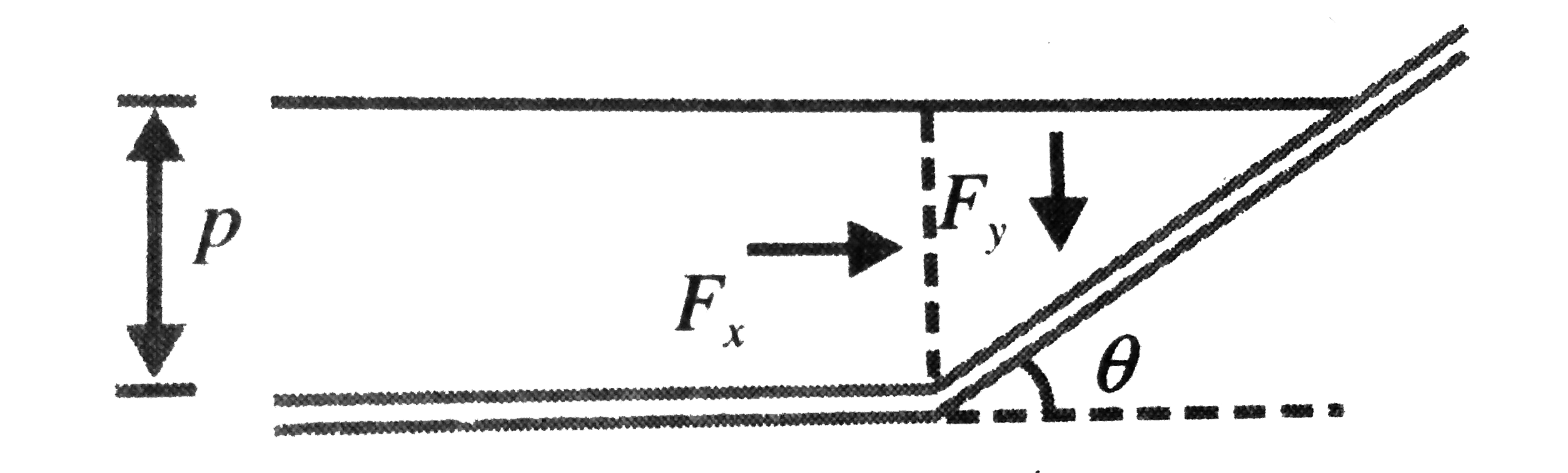
Fx=12ρghbH2
The vertical force Fv acts due to the weight of the liquid supported by the wall
Fy=12ρgb(H)(hcotθ)=12ρghH2cot2θ
The magnitude of the resultant force is
F=√F2x−F2y=12ρgbH2cosecθ
⇒Fb=12ρgH2sinθ
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.211videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.310videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples7videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Practice Problems
- Question 1 - Select One

A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k isA34MgsinθkB2MgsinθkCMgsinθkDnone of these - Question 1 - Select One
A solid cylinder of mass m rolls without slipping down an inclined plane making an angle θ with the horizontal. The frictional force between the cylinder and the incline is
AmgsinθBmgsinθ3CmgcosθD2mgsinθ3 - Question 1 - Select One
A very heavy box is kept on a frictionless incline plane inclined at an angle θ from the horizontal. Box is having an another frictionless incline plane, inclined plane as shown in the figure. A block of mass m is kept on this inclined plane inside the box. Acceleration of block w.r.t. box is
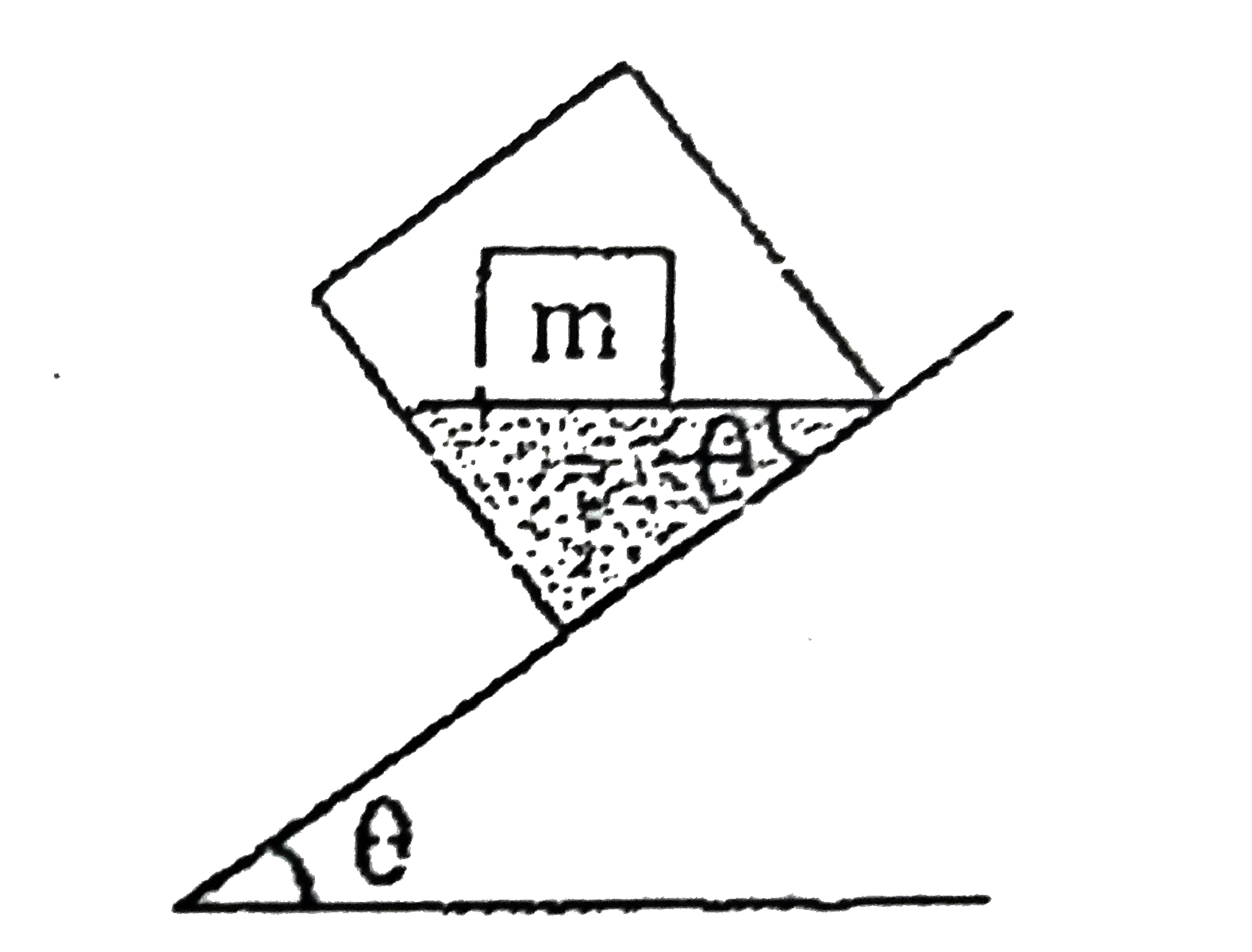 Agsin2θBgcos2θCgsinθcosθDzero
Agsin2θBgcos2θCgsinθcosθDzero - Question 1 - Select One
A string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle θ, with the string parallel to the plane, as shown in the figure. The acceleration of the disc is
 A13gsinθB12gsinθC23gsinθD13gsinθ
A13gsinθB12gsinθC23gsinθD13gsinθ - Question 1 - Select One
A trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.
 Aθ=α2Bθ=2αCθ=zeroDθ=α
Aθ=α2Bθ=2αCθ=zeroDθ=α - Question 1 - Select One
A trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.
 AEqual to αBGreater than αCEqual to α2DLesser than α
AEqual to αBGreater than αCEqual to α2DLesser than α - Question 1 - Select One
A block is at rest on an inclined plane making an angle α with the horizontal. As the angle of the incline is increased the block start slipping when the angle of inclination becomes θ then coefficient of friction is equal to
AsinθBcosθCtanθDIndependent of θ - Question 1 - Select One
A block of mass m is at rest on an incline having an angle of inclination θ with the horizontal. The incline is now being rotated with constant angular velocity ω about an axis passing through the perpendicular side. If the surface of the incline is rough having coefficient of friction as μ, then find the distance 'x' aong the incline so that block just remains stationary with restpect to incline and is on the verge of slipping. [ Take 'x' from the top of the incline as shown in the figure.]
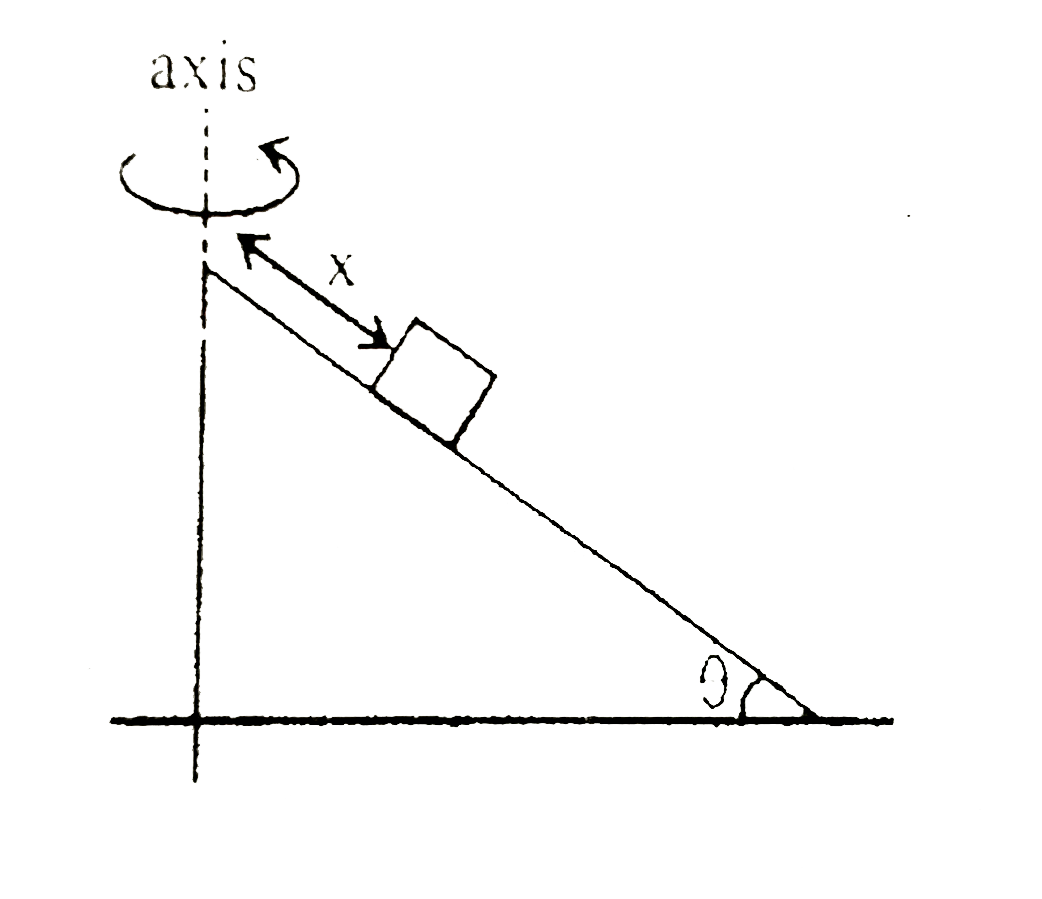 Agω2(μ+tanθ)(μtanθ−1)Bgω2(μ−tanθ)(μtanθ+1)Cgω2cosθ(μ−tanθ)(μtanθ+1)Dgω2(μ−tanθ)(μtanθ−1)
Agω2(μ+tanθ)(μtanθ−1)Bgω2(μ−tanθ)(μtanθ+1)Cgω2cosθ(μ−tanθ)(μtanθ+1)Dgω2(μ−tanθ)(μtanθ−1)
Similar Questions
A particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA solid sphere of mass M and radius R is covered with a thin shell of mass M. There is no friction between the inner wall of the shell and the sphere. The ball is released from rest, and then it rolls without slipping down an incline that is inclined at an angle θ to the horizontal. Find the acceleration of the ball.
View Solution

