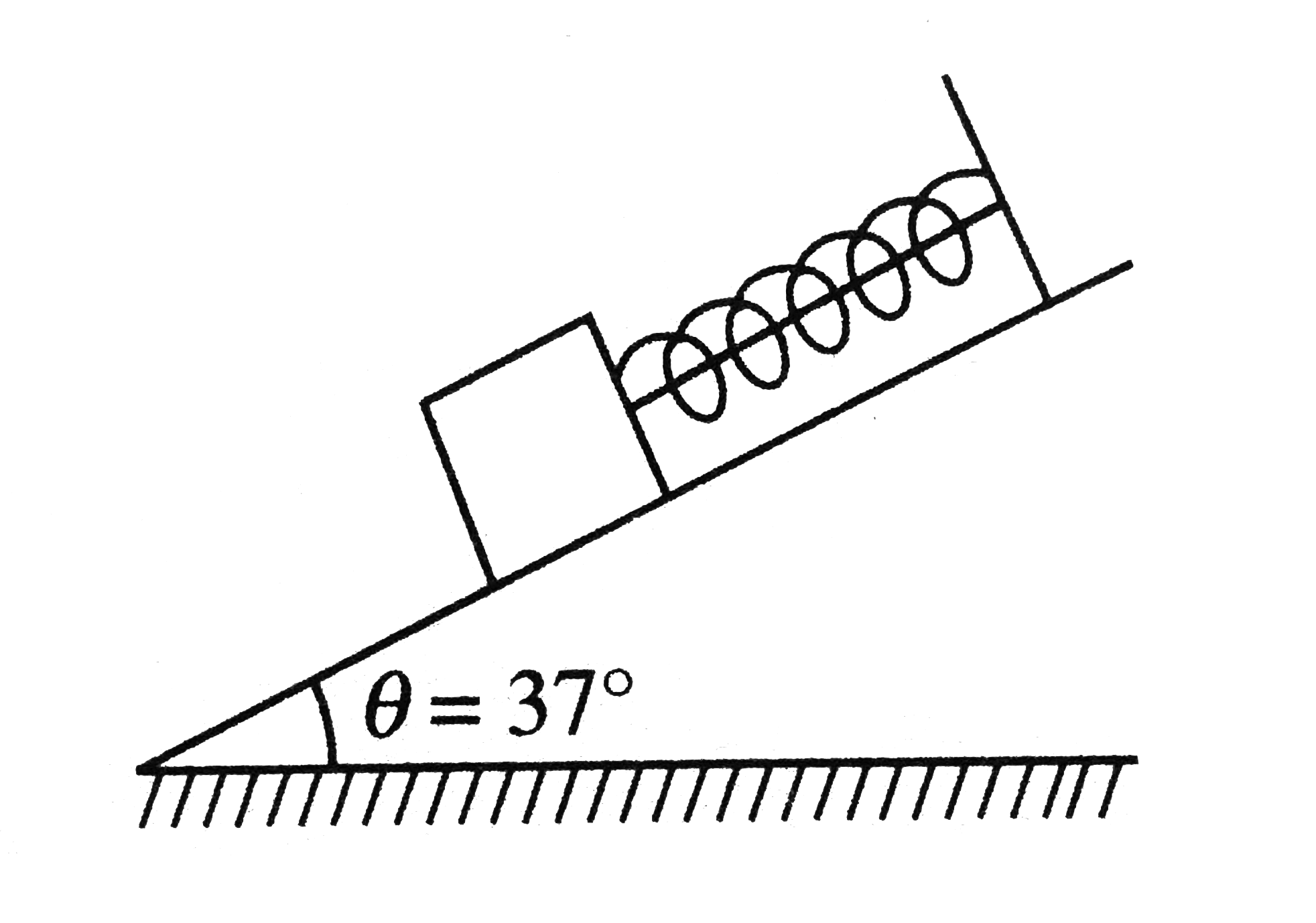
A small block of mass m=1kg is attached with one end of the spring of force constant K=110Nm−1. Other end of the spring is fixed to a rough plane having coefficient of friction μ=0.2. The spring is kept in its natural length by an inextensible thread ties between its ends as shown in figure. If the thread is burnt, calculate the elongation of the spring when the block attains static equilibrium position.
The correct Answer is:6411cm
When the string is burnt, the block starts moving down. Due to friction and spring force, the block slows down and stops. Applying work-energy theorem between points 1 and 2,
Wtotal=Δk(for block)
Wgravity+Wfriction+Wspring=Kfinal−Kinitial

mgsinθx1−μmgcosθx1−12kx21=0−0
1×10×35x1−0.2×1×10×45x1−12110×x21=0
⇒x1=0.08m or 8cm
As at position 2, we can find that there is net force on the block in upward direction, i.e.
kx1>μmgcosθ+mgsinθ
So the block will not be permanently at rest at position 2, and it will start moving up, let it stop at position (3). Now consider position 2 and 3, consider the (block+spring) a system.
Now work done by external force = change in total energy of the system.
Let at this position, there be a stretch x2 in the spring.

Wexternal=ΔE
Wfriction=ΔEgravitational+ΔEspring
−μmgcosθ(x1−x2)=mgy+[12kx22−12kx21]
−μmgcosθ(x1−x2)=mg(x1−x2)sinθ
−12k(x1−x2)(x1+x2)
−μmgcosθ=mgsinθ−12k(x1+x2)
12k(x1+x2)=mg(sinθ+μcosθ)
(x1+x2)=2mg(sinθ+μcosθ)k
x2=2mg(sinθ+μcosθ)k−x1
=2×1×10(35+0.2×45)110−0.08=6411cm
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct100videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.515videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
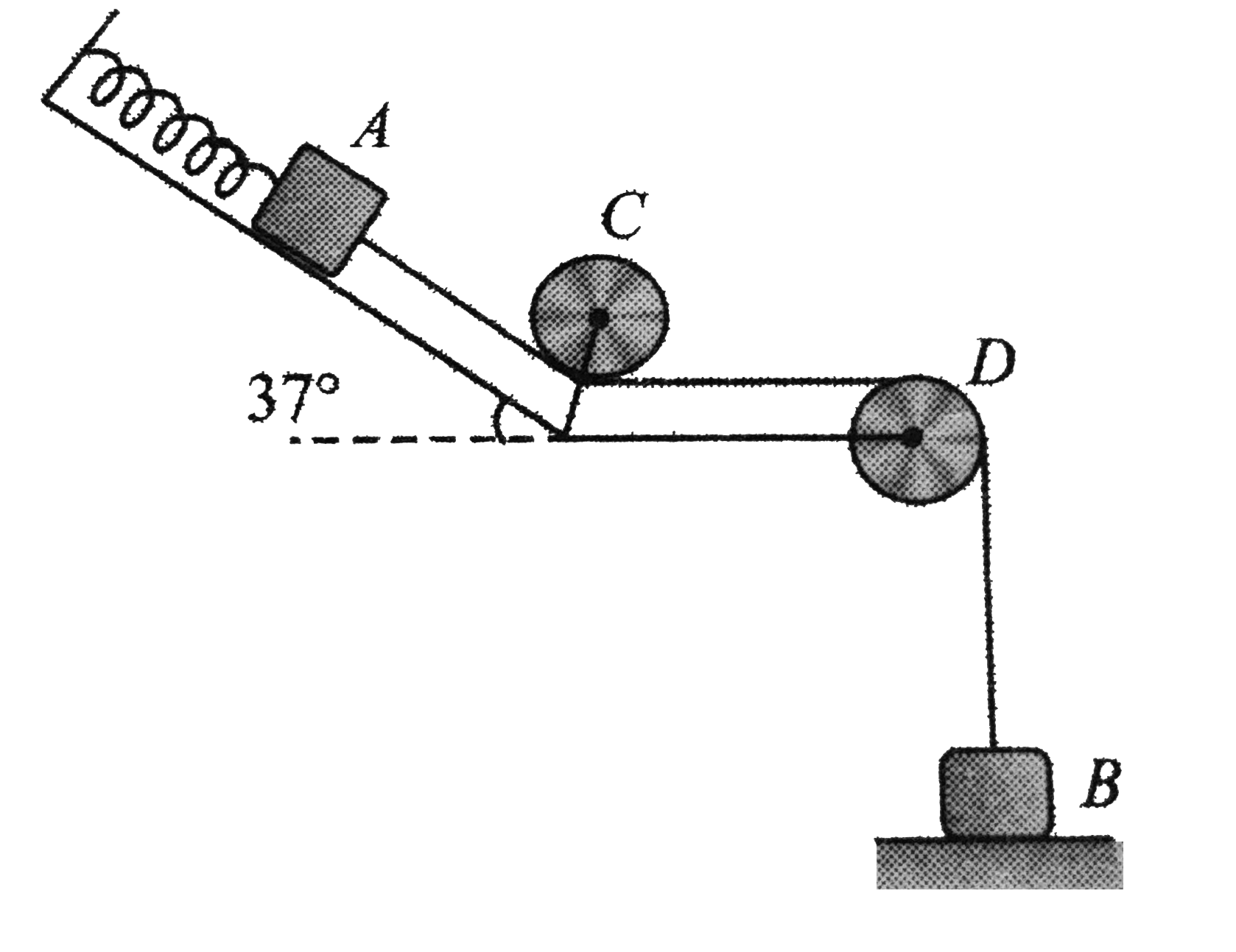
A block A of mass m=5kg is attached with a spring having force constant K=2000Nm−1. The other end of the spring is fixed to a rough plane, inclined at 37∘ with horizontal and having coefficient of friction m=0.25. Block A is gently placed on the plane such that the spring has no tension. Then block A is released slowly. Calculate elongation of the spring when equilibrium is achieved. Now an inextensible thread is connected with block A and passes below pulley C and over pulley D, as shown in figure. Other end of the thread is connected with another block B of mass 3kg. Block B is resting over a table and thread is loose. If the table collapse suddenly and B falls freely through 80/9cm, the thread becomes taut, calculate combined speed of blocks at that instant, and maximum elongation of spring in the process of motion. (g=10ms−2).
 View Solution
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of these - Question 2 - Select One
A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k - Question 3 - Select One
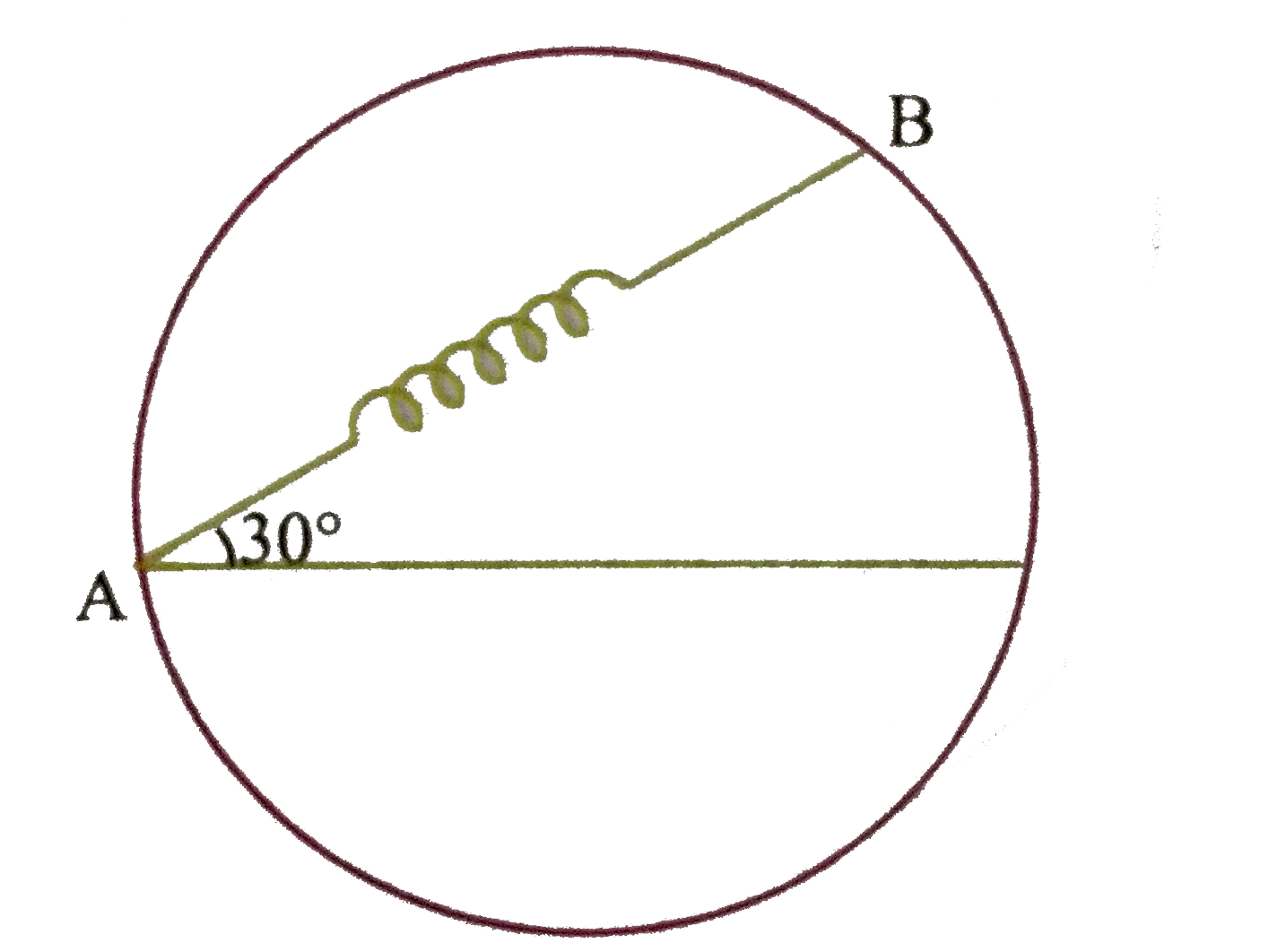
A bead of mass 'm' is attached to one end of a spring of natural length R & spring constant k=(√3+1)R. The other end of the spring is fixed at point A on a smooth vertical ring of radius R as shown. The normal reaction at B just after it is released to move is
 A√3mgB3√3mgCmg2D3√3mg2
A√3mgB3√3mgCmg2D3√3mg2
A Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
 View Solution
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 View Solution
View SolutionTwo blocks of masses m1 and m2 are attached to the lower end of a light vertical spring of force constant k. The upper end of the spring is fixed. When the system is in equilibrium, the lower block (m2) drops off. The other block (m1) will
 View Solution
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View Solution
