A parallel plate capacitor with circular plates of radius 1m has a capacitor of 1nF. At t=0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery. Calculate the magnetic field at a point P, halfway between the cnetre and the periphery of the plates, after t=10−3sec.
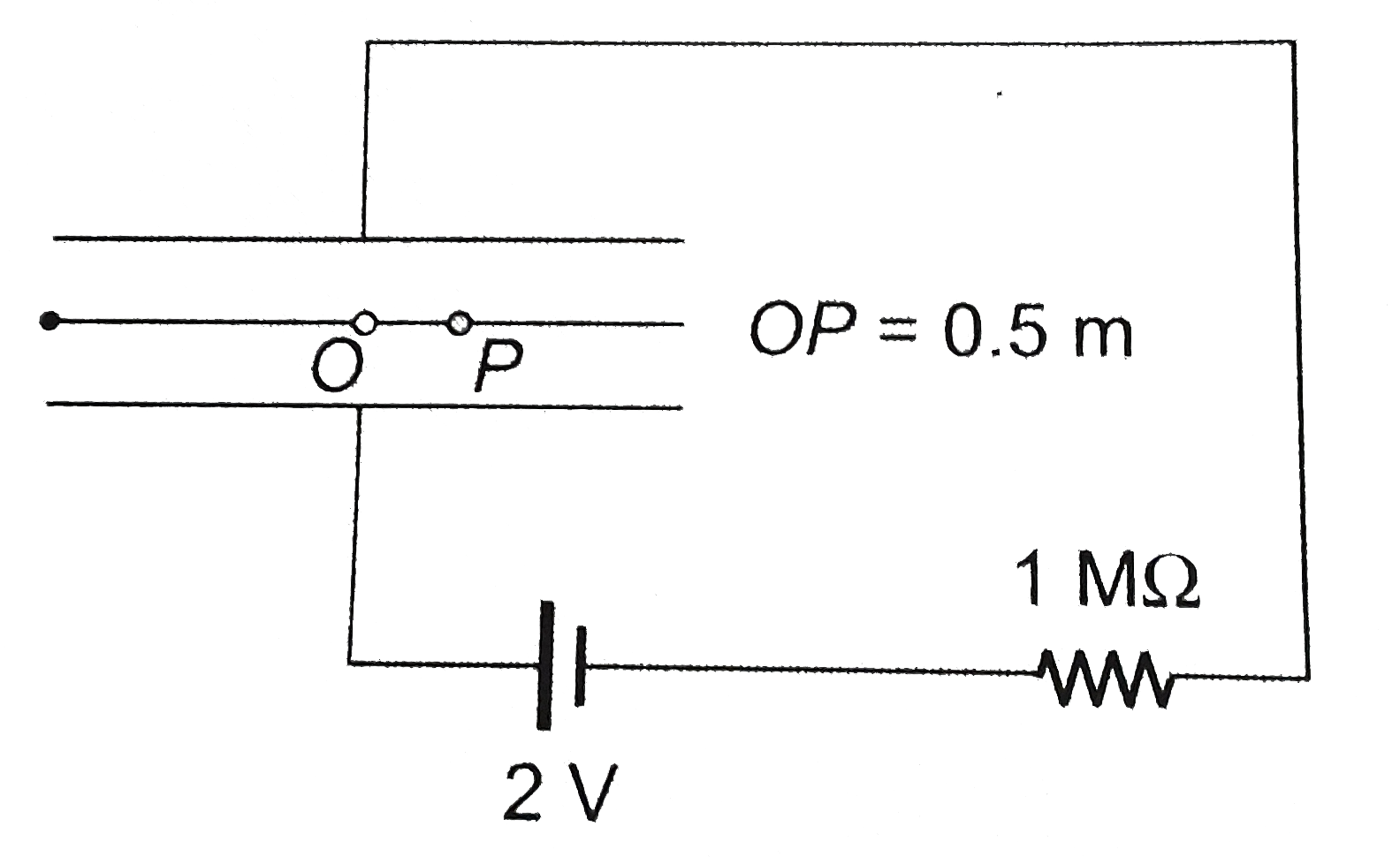
The time constant of the CR circuit is r=CR=10−3s. Then. We have
q(l)=CV[1−exp(−l/r)]
=2×10−9[1−exp(−t/10−3)]
the electric field in between the plates at time t is
E=q(t)εolon0A)=qπε∘:A=π(1)2m2= area of the plates.
Consider no a circular loop radius (1/2) m parallel to the plates passing through P. the magnetic field B at all points on the loop is along the loop and of the same value.
The flux ϕE through this loop is
ϕE=E× area of the loop
=E×π×(12)2=πE4=q4ε0
the displacement current
id=ε0dϕEdl=14dqdt=0.5×10−6exp(−1)
At t=10−3s. Now applying Ampere-Maxwell law to the loop, we get
B×2π×(12)=μ0(ic+id)=μ0(0+id)=0.5×10−6μ0 exp(-1)
or B=0.74×10−13T
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise15videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise17videos
ELECTROMAGNETIC INDUCTION
- BOOK - NCERT ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise37videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
Similar Questions
Fig. shows a capacitor made of two circular plates each of radius 12 cm and separated by 5.0mm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A.
(a) Calculate the capacitance and the rate of change of potential difference between the plates.
(b) Obtain the displacement current across the plates.
(c) Is Kirchhoff's first rule valid at each plate of the capacitor ? Explain.
 06:26View Solution
06:26View SolutionPredict the direction of induced current in the situations described by the following Figs. 6.18(a) to (f).
 02:05View Solution
02:05View SolutionTwo charges 5×10−8Cand−3×10−8C are located 16 cm apart. At what points on the line joining the two charges is the electric potential zero ? Take the potential at infinity to be zero.
12:22View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 0.5muF. At t=0, it is connected for charging inseries with a resistance R=2kOmega across a 4V battery. Calculate the magnetic field at a point P in between the plates and half way between the centre and periphery of the plates after 10^-3s . Fig.
06:26View SolutionA parallel plate capacitor is charged by connecting is plates to the terminals of a battery. The battery remains connected to the condenser plates and a glass plate is interposed between the plates of the capacitor, then
05:54View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitor of 1nF . At t = 0 , it is connected for charging in series with a resistor R = 1MOmega across a 2V battery. Calculate the magnetic field at a point P , halfway between the cnetre and the periphery of the plates, after t = 10^(-3)sec .
07:57View SolutionA parallel plate capacitor with circular plates of radius 1m has a c apacitance of 1n F. At t=0,it is connected for charging in series with a resistance R=1MΩ across2V battery . Calculate the magnetic field at a point P, in between the plates and half way between the centre and the periphery of the plates after 10−3s.
View Solutionएक समांतर प्लेट संधारित्र जिसकी व्रत्ताकार प्लेटों की त्रिज्या 1m है धारिता 1nf है। समय t = 0 पर इसको आवेशित करने के लिए R= 1 MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में 2V की बैटरी से जोडा गया है (चित्र 8.3) । 10−3s ds पश्चात संधारित्र के बीच में दोनों प्लेटों के केंद्र एवं उनकी परिमिति के ठीक मध्य में स्थित बिंदु P पर चुंबकीय क्षेत्र का परिकलन कीजिए । [क्षण t पर संधारित्र पर आवेश q(t)=CV[1–exp(−t/π)] होता है जहाँ समय नियतांक τ=CR है ]।
 View Solution
View Solutionकिसी समांतर प्लेट संधारित्र की वृत्ताकार प्लेटो की त्रिज्या 1 m तथा धारिता C=1nF है। इसे चित्र 1।9 के अनुसार 2 V की बैटरी तथा 1MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में जोड़ा गया है। आवेशित करने के लिए सलंगन स्विच को समय t = 0 पर बंद किया जाता है समय t=1ms पर संधारित्र के बीच में दोनों प्लेटो के केंद एव उसकी परिमिति के ठीक माध्य में स्थति बिंदु P पर चुंबकीय क्षेत्र का मान ज्ञात करे। मान ले कि आवेशन के क्रम संधारित्र पर आवेश का तात्कालिक मान है- q(t)CV(1−etCR)
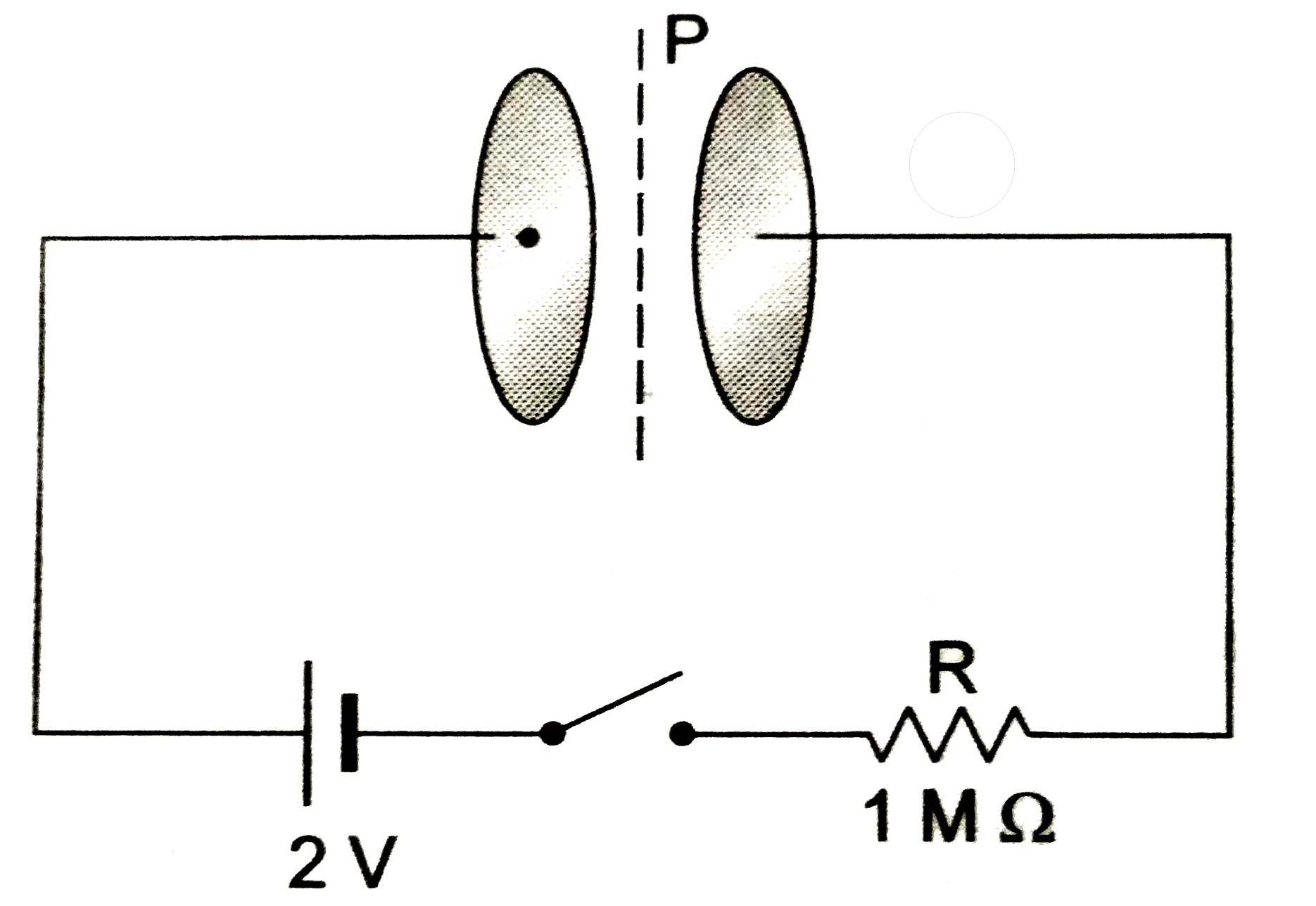 10:46View Solution
10:46View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 1 nF. At t=0 , It is connected for charging in series with are resistor R=1 M Q across a 2V battery (fig). Calculate the magnetic field at a point P halfway between the centre and the periphery of the plates. after t=10−3s. (The charge on the capacitor at time τ is q(t) CV [1 =exp (−t/τ) ], where the time constant τ is equal to CR).
View Solutionएक समांतर प्लेट संधारित्र जिसकी वृताकार प्लटो की त्रिज्या 1m है धारिता 1nF है समय t =0 पर इसको आवेशित करने के लिए R=1MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में 2V की बैटरी से जोड़ा गया है ( चित्र ) 10−3S के पश्चात संधारित्र के बीच में दोनों प्लेटो के केंद्र एवं परिकलन कीजिए [क्षण t पर संधारित्र पर आवेश q(t)=CV[1−exp(−t/t) होता है जहाँ समय नियतांक τ=CR है
 12:07View Solution
12:07View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 1nF. At t = 0, it is connected for chargeing in series with a resistor R=1 M Omega across a 2V battery (Figure). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10^(-3)s . (The charge on the capacitor at time t is q(t)=CV[1-exp((-t)/(tau))] , where the time constant tau is equal to CR).
07:32View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)
 04:52View Solution
04:52View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)
 08:50View Solution
08:50View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)
 07:32View Solution
07:32View Solution

