Assertion $(A) :$ In radioactive disintegrations, $._{2} H^{4}$ nuclei can come out of the nucleus but lighter $._{2} H^{3}$ cannot.
Reason $(R) :$ The binding energy of $._{2} H^{3}$ is more than that of $._{2} H^{4}$ .

A

If both $(A)$ and $(R)$ are correct , and $(R)$ is the correct explanation of $(A)$

B

If both $(A)$ and $(R)$ are correct, but (R) is not the correct explanation of $(A)$

C

If $(A)$ is correct, but $(R)$ is incorrect.

D

If $(A)$ is incorrect, but $(R)$ is correct.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Radioactive disintegration reaction produces stable nuclei, till that the nuclei undergo the process. The $._{2} H e^{4}$ nuclei is more stable than $._{2} H e^{3}$ nuclei. Hence, it is proceed in radioactive reaction.

Updated on:21/07/2023

|

Class 12 CHEMISTRY CHEMICAL KINETICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Assertion $(A) :$ In radioactive disintegrations, $._{2} H e^{4}$ nuclei can come out of the nucleus but lighter $._{2} H^{3}$ cannot.
Reason $(R) :$ The binding energy of $._{2} H^{3}$ is more than that of $._{2} H^{4}$ .
ASTATEMENT-1 is True, STATEMENT-2 is True, STATEMENT-2 is correct explanation for STATEMENT-1
BSTATEMENT-1 is True, STATEMENT-2 is True, STATEMENT-2 is NOT a correct explanation for STATEMENT-1
CSTATEMENT-1 is True, STATEMENT-2 is False
DSTATEMENT-1 is False, STATEMENT-2 is True
Assertion : Bond angle in $H_{2} O$ is less than that in $H_{2} S$ .
Reason : Electronegativity of O is more than that of S.
AAssertion and reason both are correct statements and reason is correct explanation for assertion.
BAssertion and reason both are correct statements but reason is not correct explanation for assertion.
CAssertion is correct statement but reason is wrong statement.
DAssertion is wrong statement but reason is correct statement.
Assertion (A):
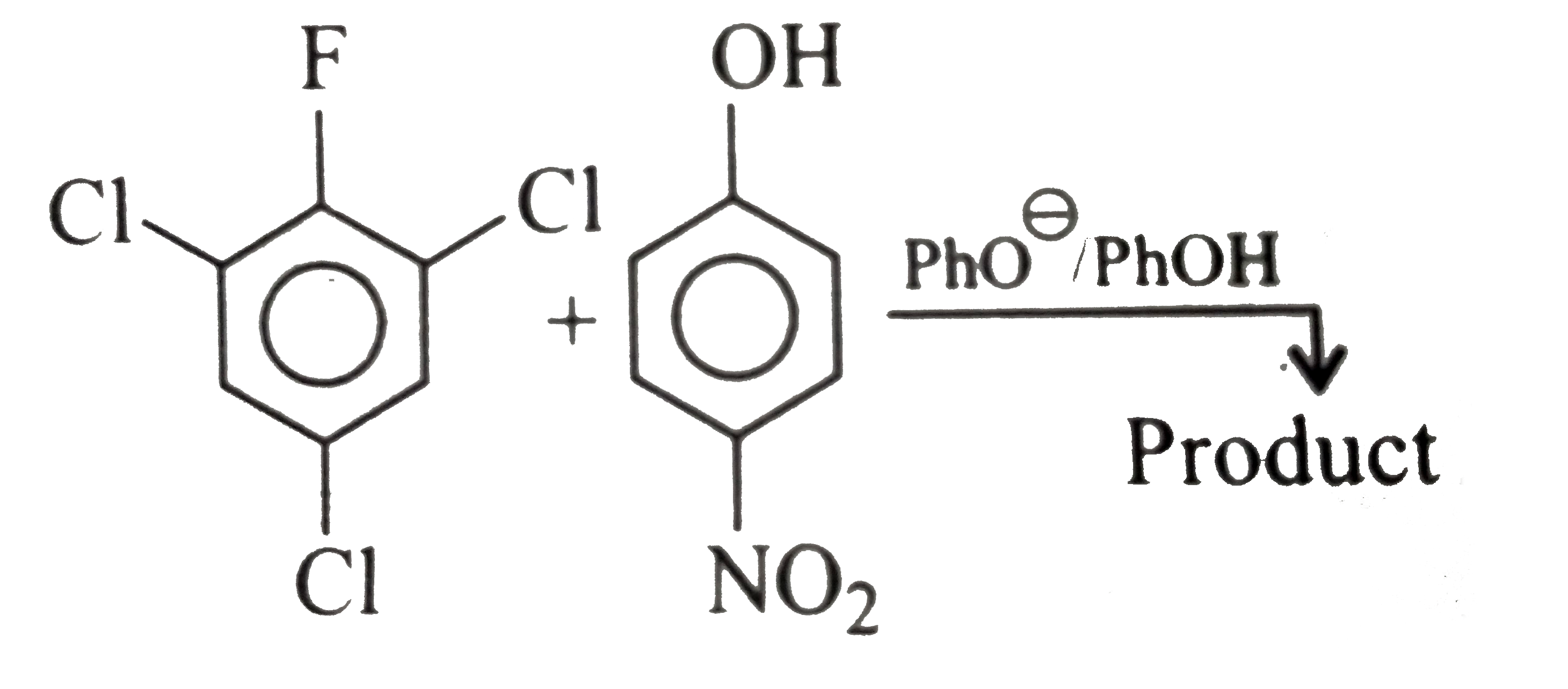
The product is: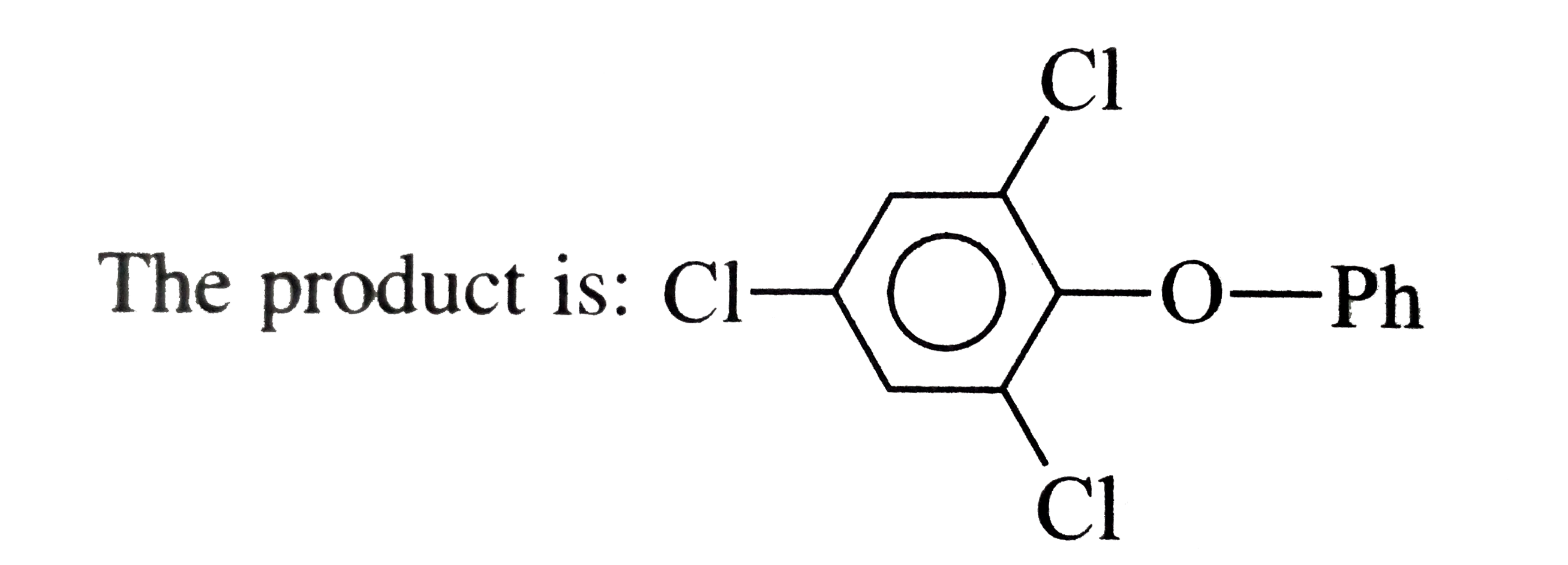
Reason (R ): $p - N O_{2} - C_{6} H_{4} O^{-}$ is a stronger nucleophile than $P h O^{-}$ .
AIf both (A) and (R ) are true and (R ) is the correct explanation of (A).
BIf both (A) and (R ) are true but (R ) is not the correct explanation of (A).
CIf (A) is true but (R ) is false.
DIf both (A) and (R ) are false.

CENGAGE CHEMISTRY-NUCLEAR CHEMISTRY-Exercises Assertion-Reasoning

Home
Ask Doubt
Profile